Le système thermodynamique considéré dans cette partie est constitué de
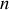moles de gaz parfait. Ce gaz parfait est confiné dans un cylindre vertical clos dans sa partie supérieure par un piston de masse
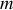et de surface
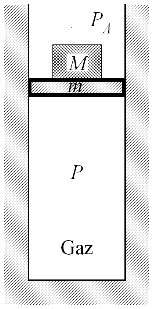
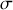. L'ensemble est isolé du point de vue thermique, mais pas du point de vue mécanique. Le piston est en effet susceptible de se déplacer. Ce déplacement est supposé se produire sans frottement. Dans l'état d'équilibre initial, le gaz occupe le volume
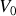, à la pression
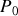et à la température ambiante
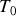. On nomme
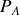la pression atmosphérique extérieure.
Question 1
Calculer la valeur de
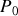en fonction de
,
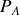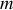et
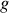(accélération de la pesanteur).
Question 2 : Compression ou détente par ajout ou retrait d'un poids
On place sans heurt une masse
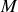sur le piston.
a) Décrire et caractériser la transformation qui se produit.
b) Calculer la pression finale
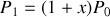, où
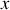est fonction de
,
,
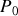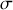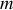et
.
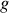c) Exprimer le transfert thermique
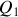et la variation d'entropie
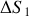du gaz parfait en fonction de
,
,
,
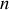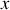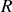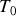, du coefficient de Laplace
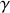et de la température finale
.
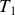d) Exprimer la quantité de travail
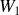échangée à l'issue de la transformation et en déduire la variation d'énergie interne
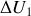du gaz parfait en fonction de
,
,
,
,
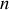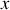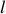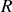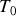et
.
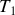e) Par application de la première loi de Joule, déduire
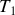et
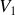, température et volume finaux, en fonction de
,
,
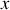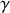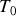ou
.
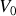f) Effectuer un développement limité au deuxième ordre en
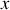de la variation d'entropie de « l'Univers » (également nommée « entropie créée » ou « entropie irréversible ») au cours de la transformation en fonction de
,
,
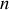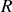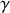, et
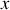. En quoi ce résultat confirme-t-il vos conclusions du a) ?
g) Que se passe-t-il si, ensuite, l'on retire
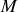? Le système revient-il à son état initial
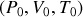? Dans le cas contraire, la température finale
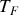est-elle plus grande ou plus petite que
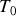? (Ou : l'opérateur a-t-il apporté de l'énergie au système ?)
Question 3 : Compression par ajout progressif de petits poids
Après avoir fait revenir le système à
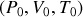, son état initial, on ajoute progressivement de petites surcharges afin de comprimer le gaz jusqu'à la pression
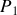précédemment calculée (et les volume
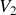et température
).
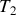a) Quelle est la masse totale alors ajoutée ?
b) Comment peut-on ici caractériser la transformation ?
c) Déduire de la loi de Laplace les valeurs de
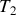et
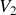en fonction de
,
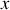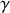et
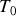ou
.
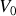d) Calculer
,
,
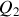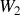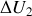et
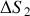en fonction de
,
,
,
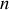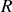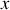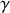et
.
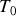e) Montrer, en effectuant un développement limité de
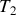et
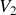dans le cas où
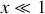, que l'on peut alors identifier
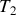et
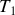d'une part,
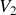et
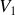d'autre part. Que peut-on conclure de ces résultats ?
