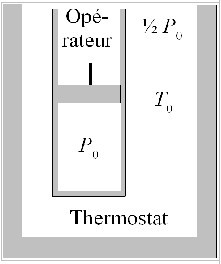
On considère maintenant une mole du même gaz parfait enfermé dans un cylindre vertical, muni d'un piston de masse négligeable et coulissant sans frottement. Les parois du cylindre et du piston sont diathermes (ou diathermanes, i.e. thermiquement perméables). L'ensemble du système se trouve au contact d'un thermostat à
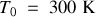. Le volume initial du gaz est égal à
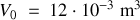et sa pression initiale est égale à
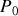, soit deux fois la pression de l'atmosphère extérieure (
).
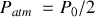Le piston est initialement bloqué par l'opérateur.
Question 1
L'opérateur relâche très lentement le piston. La pression diminue progressivement jusqu'à atteindre la valeur de la pression atmosphérique,
a) Caractériser cette transformation.
b) Déterminer l'état final
,
,
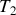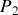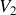. Effectuer les applications numériques.
c) Déterminer la variation d'énergie interne
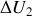, les travail des forces de pression
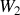et transfert thermique
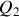. Faire l'application numérique.
d) Exprimer puis calculer la variation d'entropie
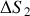du gaz lors de cette détente.
e) Exprimer puis calculer la variation d'entropie du thermostat
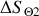lors de cette détente, puis la variation de l'entropie de l'Univers
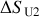. Conclure.
Question 2
L'opérateur lâche brusquement le piston (en partant du même état initial qu'à la question 1). Dans un premier temps, les transferts thermiques n'ont pas le temps de se produire et le piston atteint une certaine hauteur. On constate ensuite qu'il continue à monter lentement jusqu'à la position d'équilibre.
a) Caractériser cette transformation, et notamment les deux étapes de celle-ci.
b) Déterminer la variation d'énergie interne
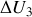, les travail des forces de pression
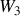et transfert thermique
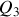. Effectuer les applications numériques.
c) Exprimer et calculer la variation d'entropie
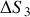du gaz lors de cette détente.
d) Exprimer et calculer la variation d'entropie du thermostat
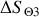lors de cette détente, puis la variation de l'entropie de l'Univers
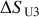. Conclure.
