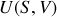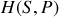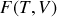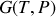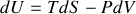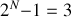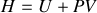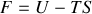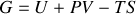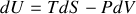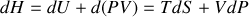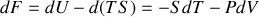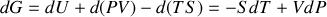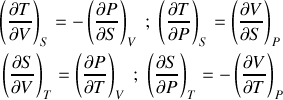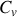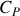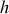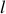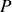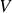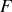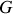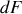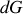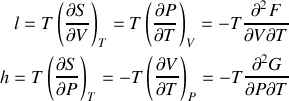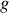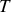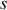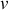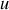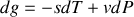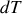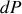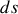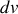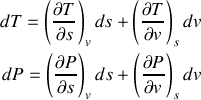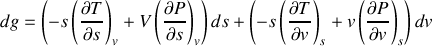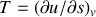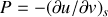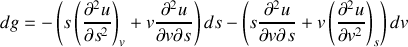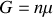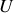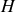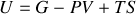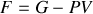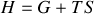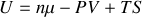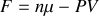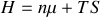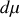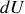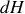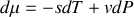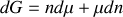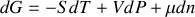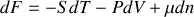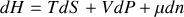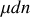Relations mathématiques

Soit l'énergie interne d'un système fermé. À partir d'une analyse des termes intervenant dans la relation fondamentale de la thermodynamique, appliquer les transformations de Legendre qui permettent d'en déduire l'enthalpie , l'énergie libre et l'enthalpie libre .

Écrire les différentielles des quatre fonctions précédentes pour un système fermé. Par application des égalités de Schwarz, en déduire les relations de Maxwell.

Un transfert thermique quasi-statique peut s'écrire en raison des capacités thermiques absolues ou du système considéré et des coefficients thermométriques et :

À quoi les coefficients thermiques et sont-ils égaux en fonction de dérivées partielles de et ?(Utiliser les relations de Maxwell pour ces relations de Clapeyron). Même question en fonction de dérivées partielles mixtes de et .

L'enthalpie libre molaire s'exprime simplement en fonction de et . Exprimer sa différentielle en fonction du choix de paramètres et et des dérivées partielles de second ordre correspondantes de l'énergie interne molaire . Ce choix de variables et est-il pertinent ?

Considérons maintenant un système ouvert. L'enthalpie libre s'exprime aisément en fonction du nombre de moles et du potentiel chimique : . Déduire par transformation de Legendre les expressions de , et .

Quelle est l'expression différentielle du potentiel chimique en fonction des variables et  ? En déduire les expressions différentielles , , , sous la forme d'une somme de trois termes : un premier de type thermique, un autre de travail mécanique et un troisième de travail chimique.