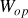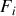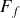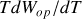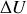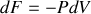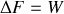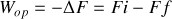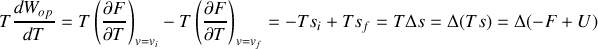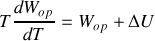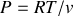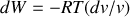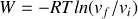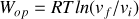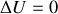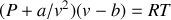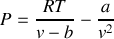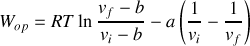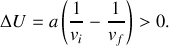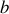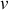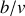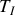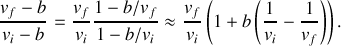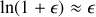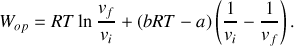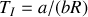Énergie libre et « isochore de van't Hoff »
Au cours de la détente quasi-statique isotherme d'une mole de gaz maintenue à la température
 par un thermostat, ce gaz fournit un travail
par un thermostat, ce gaz fournit un travail
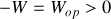 à un opérateur extérieur. Si les volumes initial
à un opérateur extérieur. Si les volumes initial
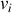 et final
et final
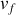 sont donnés, il est possible de définir ce travail isotherme comme une fonction
sont donnés, il est possible de définir ce travail isotherme comme une fonction
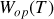 de la température entre deux isochores (
de la température entre deux isochores (
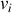 et
et
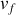 ). On se propose d'en étudier la loi de variation.
). On se propose d'en étudier la loi de variation.
Question
Isochore de van't Hoff |
|---|
Exprimer
|
Question
Cas du gaz parfait |
|---|
Calculer
|
Question
D'où vient en dernière instance l'énergie fournie à l'opérateur ? |
Question
Cas du gaz de van der Waals |
|---|
Calculer
|
Question
Écrire l'isochore de van't Hoff pour le gaz de van der Waals à la température
|
Question
Montrer que, dans le cas des basses pressions (lorsque le covolume molaire
|