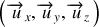Dans le repère d'espace 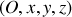défini précédemment (voir figure 3), un point 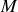est repéré par ses coordonnées d'espace 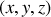correspondant à la mesure algébrique de la projection de M successivement sur les 3 axes du repère. Ces 3 coordonnées sont de même nature et homogènes à une longueur.

La base orthonormée associée à ce système d'axe est notée 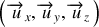. C'est une base qui ne change pas au cours du temps : ces vecteurs gardent la même direction, le même sens et la même norme au cours du temps. On dit encore que la base est fixe dans le repère. Ces vecteurs peuvent être représentés n'importe où dans l'espace mais en général ils sont représentés au point origine .

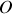La connaissance du vecteur position 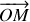permet aussi de repérer le point 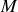. Les composantes de ce vecteur, dans la base cartésienne 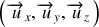correspondent aux coordonnées du point :

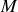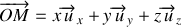(1)

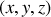sont les coordonnées cartésiennes du point .

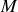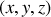sont les composantes du vecteur position 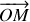dans la base cartésienne