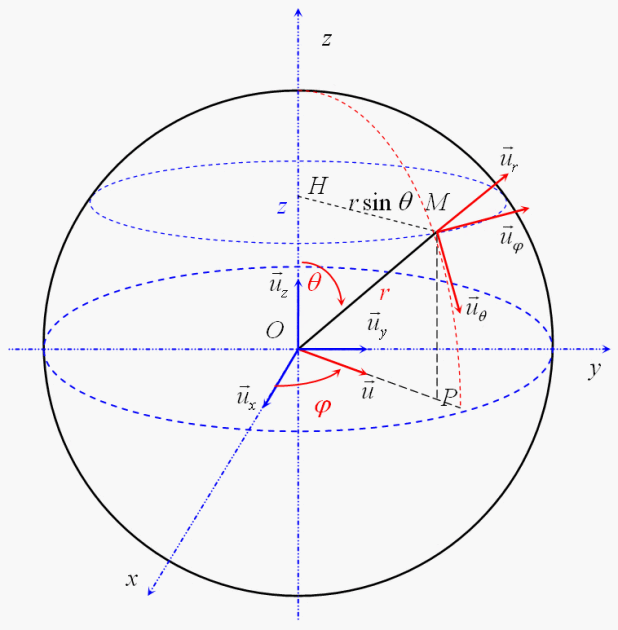
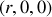Définition
Les coordonnées sphériques (voir figure 6) permettent de repérer un point sur une sphère de rayon
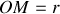 . C'est typiquement le repérage d'un point sur la Terre pour lequel il suffit alors de préciser deux angles : la latitude et la longitude.
. C'est typiquement le repérage d'un point sur la Terre pour lequel il suffit alors de préciser deux angles : la latitude et la longitude.
Figure 6 : Le système de coordonnées sphériques
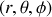 et la base associée
et la base associée
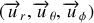
Coordonnées sphériques
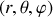 :
:
La coordonnée radiale
 correspond à la distance de l'origine
correspond à la distance de l'origine
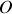 du repère au point
du repère au point
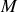 .
.
La coordonnée angulaire
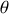 correspond à l'angle que fait
correspond à l'angle que fait
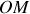 avec l'axe
avec l'axe
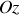 . Cet angle, compris entre
. Cet angle, compris entre
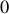 et
et
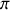 , est appelé colatitude (angle complémentaire de la latitude) ou zénith.
, est appelé colatitude (angle complémentaire de la latitude) ou zénith.
La coordonnée angulaire
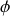 correspond à l'angle que fait le plan défini par l'axe
correspond à l'angle que fait le plan défini par l'axe
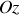 et
et
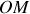 avec l'axe
avec l'axe
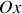 . Cette angle, compris entre
. Cette angle, compris entre
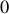 et
et
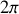 , est appelé la longitude ou l'azimut.
, est appelé la longitude ou l'azimut.
La base des coordonnées sphériques
Le vecteur position permet de définir le premier vecteur de la base :

Le vecteur unitaire
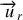 est suivant la direction et le sens de
est suivant la direction et le sens de
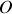 vers
vers
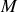 : c'est le vecteur radial (suivant le rayon).
: c'est le vecteur radial (suivant le rayon).
Lorsque seul l'angle
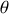 varie le point
varie le point
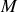 décrit un demi-cercle (un méridien) de rayon
décrit un demi-cercle (un méridien) de rayon
 . Le vecteur unitaire
. Le vecteur unitaire
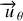 est tangent à ce demi-cercle (suivant le méridien) orienté comme
est tangent à ce demi-cercle (suivant le méridien) orienté comme
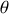 .
.
Lorsque seul l'angle
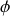 varie le point
varie le point
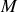 décrit un cercle de rayon
décrit un cercle de rayon
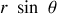 . Le vecteur unitaire
. Le vecteur unitaire
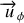 est tangent à ce cercle (suivant un parallèle) orienté comme
est tangent à ce cercle (suivant un parallèle) orienté comme
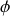 .
.
Les vecteurs
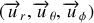 forment une base orthonormée directe. Cette base est « mobile » dans le repère.
forment une base orthonormée directe. Cette base est « mobile » dans le repère.
Relation entre les coordonnées sphériques et cartésiennes
La projection
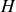 du point
du point
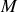 sur l'axe
sur l'axe
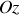 donne la cote :
donne la cote :
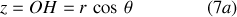
Si
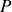 est la projection de
est la projection de
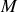 sur le plan
sur le plan
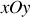 on a :
on a :
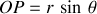
Les coordonnées
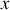 et
et
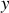 du point
du point
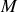 sont celles du point
sont celles du point
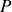 c'est à dire :
c'est à dire :
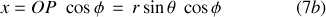
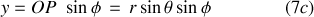
Le vecteur unitaire
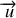 suivant
suivant
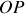 a pour expression :
a pour expression :
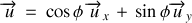
Le vecteur unitaire
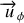 est directement perpendiculaire à
est directement perpendiculaire à
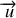 . Il fait un angle
. Il fait un angle
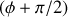 avec l'axe
avec l'axe
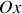 et s'écrit :
et s'écrit :
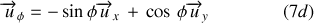
Le vecteur unitaire
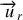 a pour expression :
a pour expression :
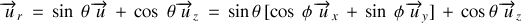
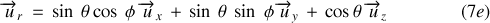
Enfin, le vecteur unitaire
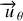 est directement perpendiculaire à
est directement perpendiculaire à
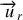 et s'écrit :
et s'écrit :
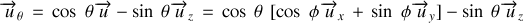
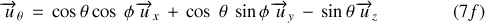
Attention :
Les coordonnées sphériques du point
 sont :
sont :
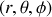
Les composantes du vecteur position
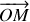 sont :
sont :