Définition
Le point
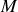est parfaitement repéré si on connaît la distance
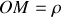(lettre grecque rhô) et l'angle
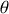(lettre grecque thêta) que fait le segment
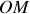avec l'axe
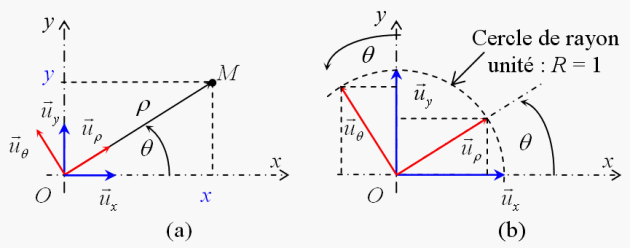
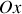(voir figure 4 (a)).
Figure 4 : Les coordonnées polaires
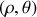et la base associée
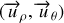
La longueur du segment
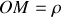correspond à la coordonnée radiale (notée
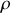ou
). L'angle
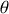est la coordonnée angulaire. Cet angle est mesuré par rapport à l'axe des abscisses
.
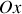Attention :
Contrairement aux coordonnées cartésiennes
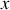et
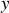, les coordonnées polaires
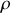et
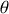ne sont pas de même nature. La coordonnée radiale
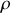a la dimension d'une longueur comme
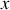et
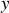. La coordonnée angulaire
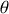s'exprime en radian (unité d'angle sans dimension).
La base polaire
Le vecteur position
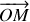peut s'écrire :
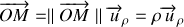
Le vecteur unitaire
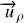est suivant la direction et le sens de
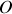vers
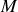: c'est le vecteur
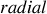(suivant le rayon).
Une nouvelle base orthonormée directe (
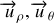) est obtenue en associant à
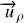le vecteur unitaire
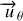directement perpendiculaire (dans le sens trigonométrique) : c'est le vecteur orthoradial (perpendiculaire au rayon) (voir figure 4 (b)).
La base du système de coordonnées polaires
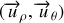est une base définie à partir de la position du point
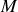. Si le point est en mouvement le vecteur
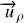(et par conséquent
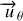) change de direction : la base est « mobile » dans le repère. Ces vecteurs peuvent être représentés n'importe où dans l'espace mais ils sont représentés souvent soit au point origine
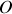soit au point
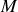lui-même.
Attention :
Ne pas confondre coordonnées polaires du point et composantes du vecteur position de ce même point.
Les coordonnées polaires du point
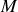sont : (
)
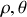Les composantes du vecteur position
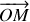sont : (
)
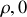Relation entre les coordonnées polaires et cartésiennes
Avec les notations de la figure 4, les relations entre les systèmes de coordonnées cartésiennes et polaires sont :
Passage polaires
cartésiennes
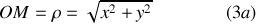
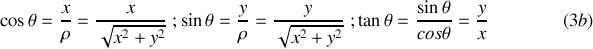
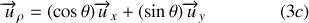
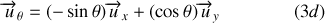
Passage cartésiennes
polaires
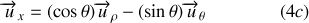
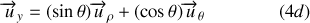
Attention :
Si l'étude est effectuée en coordonnées cartésiennes seules doivent apparaître les grandeurs (
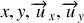). En coordonnées polaires n'apparaîtront que les grandeurs
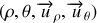. Il ne faut en aucun cas conserver des expressions comportant un mélange de ses grandeurs.
