Puisque l'équation fondamentale de la statique des fluides permet d'évaluer la pression en tout point d'un fluide, il est possible de calculer les forces s'exerçant sur les parois d'un solide totalement ou partiellement immergé. On sait que la force de pression agissant sur un élément de surface 
s'exprime 
. Sur une surface immergée 
, la force hydrostatique totale s'obtient en calculant :
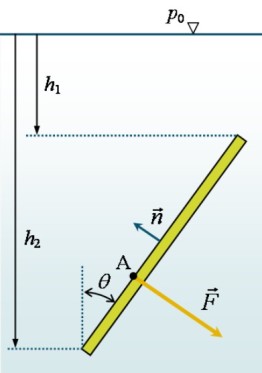
Si l'on considère le cas particulier simple d'une plaque plane totalement immergée (voir figure 4), la force hydrostatique s'exerçant sur la face supérieure est portée par la normale 
à cette surface :
où 
est la largeur de la plaque (suivant la perpendiculaire au plan du schéma), et 
est l'angle d'inclinaison de la plaque par rapport à la verticale. Si 
est la profondeur à partir d'un niveau de référence (surface libre) où la pression est la pression atmosphérique 
, pour une unité de largeur 
, on obtient l'équation suivante :
soit encore :
On remarque alors que 
et que 
, où 
correspond à la profondeur du barycentre de la surface 
. Par conséquent, il vient :
Ce résultat peut être généralisé à n'importe quelle surface immergée, quelle que soit sa forme : pour évaluer 
il suffit donc de connaitre sa surface 
et la profondeur de son barycentre 
.
Remarque :
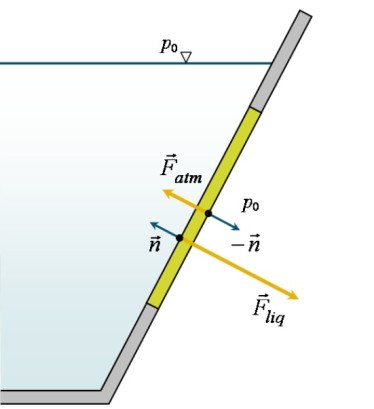
Dans le cas d'une paroi séparant un liquide de l'atmosphère (figure 5), la résultante des forces de pression s'affranchit du terme dû à la pression atmosphérique : en effet, la pression 
exerce une force 
qui s'oppose à la force due au liquide 
. Par conséquent, la force résultante s'exerçant sur la paroi se résume à 
.
Complément :
Une justification logique et moins formelle consiste à voir que la pression atmosphérique s'exerce de part et d'autre de la paroi (elle agit notamment du côté immergé par l'intermédiaire de la surface libre).
Dans la plupart des problèmes, il est également nécessaire de connaître le point d'application
A de la force hydrostatique. Il se détermine par le calcul du moment de la force 
par rapport à un point O quelconque :
où M est un point qui balaye toute la surface 
. Cette égalité vectorielle permet alors d'obtenir 
, et donc la position du point d'application A.
Exemple :
A titre d'illustration, on peut calculer le point d'application A de la force hydrostatique 
s'exerçant sur la paroi de surface 
d'un récipient contenant une hauteur 
de liquide (figure 6).
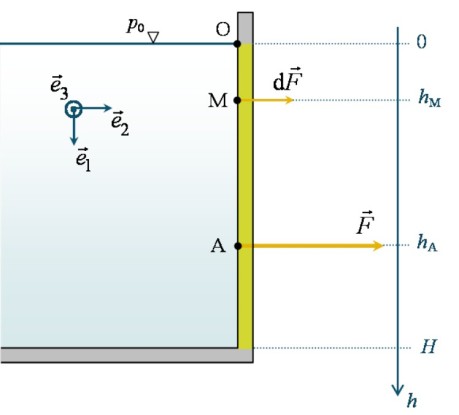
Compte tenu du fait que la pression atmosphérique agit de part et d'autre de la paroi, on pourra s'affranchir de son écriture dans la formulation du problème. Ainsi, on sait que 
et en choisissant arbitrairement un point O situé sur la paroi à l'interface atmosphère-liquide, on pose :
où 
et 
, ce qui conduit à :
On exprime alors la distance OA (profondeur 
du point d'application) comme :
On pourra par ailleurs généraliser ce résultat en vérifiant qu'il est indépendant de l'inclinaison de la paroi.
Attention :
Bien que le point O puisse être choisi de manière totalement arbitraire, il est logique de le choisir de sorte que les calculs soient les plus simples possible ; généralement, il convient par exemple de choisir O appartenant à la surface d'intégration, sur l'une de ses extrémités (comme dans l'exemple traité précédemment).
