Il est possible d'effectuer le calcul de la force hydrostatique s'exerçant sur une surface fermée, celle-ci délimitant un volume totalement ou partiellement immergé. Dans ce cas, la force est appelée poussée d'Archimède. Cette poussée s'exprime :

Figure 7

Tirée de la formule d'Ostrogradski, la formule du gradient permet de transformer une intégrale surfacique en une intégrale volumique :

On peut donc ici remplacer la grandeur scalaire par la pression , ce qui donne :

Or, le fluide étant au repos, l'équation fondamentale de la statique des fluides permet d'écrire que , d'où la nouvelle expression de la poussée d'Archimède :

Et comme peut être considérée constante sur tout le volume, si le liquide est incompressible ( est aussi constant sur tout le volume) on obtient alors :

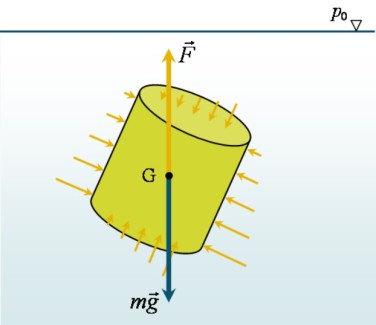
Autrement dit, la poussée d'Archimède est une force qui s'exerce dans la direction opposée à et dont l'intensité est égale au poids du liquide déplacé par le volume immergé (figure 7).

Ainsi, les conditions de flottaison (conditions d'équilibre) sont régies par la différence d'intensité entre les deux forces en présence (poids propre de l'objet immergé et poussée d'Archimède).

Sans en faire la démonstration, on admettra que le point d'application de la poussée d'Archimède est le barycentre du volume immergé.