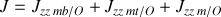Le pendule est constitué de plusieurs éléments : la bague, la tige et la masse. Chacun de ses éléments contribue au moment d'inertie du pendule qui tourne autour d'un seul axe de rotation
 passant par
passant par
 perpendiculaire au plan de la feuille. Si la longueur de la tige
perpendiculaire au plan de la feuille. Si la longueur de la tige
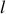 est bien supérieure à son rayon
est bien supérieure à son rayon
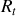 , le moment d'inertie de la tige par rapport à son centre de masse
, le moment d'inertie de la tige par rapport à son centre de masse
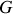 est donné par
est donné par
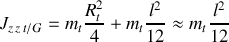
Par application du théorème de Huygens, on obtient le moment d'inertie de la tige par rapport à
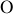
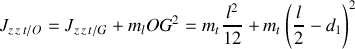
Un calcul similaire s'applique à la masse
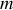 située à la distance
située à la distance
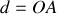 de l'axe de rotation. Cette masse cylindrique de rayon
de l'axe de rotation. Cette masse cylindrique de rayon
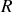 et hauteur
et hauteur
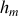 étant très lourde, on ne fera pas d'approximation. Il s'ensuit que
étant très lourde, on ne fera pas d'approximation. Il s'ensuit que
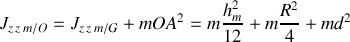
La bague étant quasi ponctuelle, on admettra que son moment d'inertie est donné par
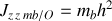
Fondamental :
Le moment d'inertie complet du pendule est donc donné par