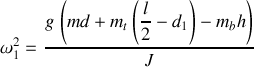Pour le pendule pesant non couplé, il suffit d'appliquer le théorème des moments en
pour trouver l'équation différentielle du mouvement du pendule. Les forces qui agissent sur le pendule son la réaction de l'axe en
, le poids de la barre en
, le poids de la bague en
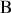et le poids de la masse en
.
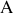Le théorème des moments s'écrit donc
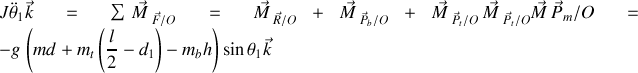
Il s'ensuit que l'équation différentielle du mouvement est donnée par
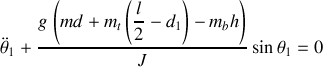
Remarque :
Pour des mouvements de faible amplitude cette équation devient linéaire et correspond à celle d'un oscillateur harmonique du type
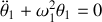avec
