Comme les équations différentielles du mouvement sont linéaires, la solution générale est une combinaison linéaire des modes normaux, i.e.

et pour la vitesse angulaire

Supposons qu'à
 ,
,
 ,
,
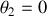 et que les pendules soient initialement au repos. Il s'ensuit que
et que les pendules soient initialement au repos. Il s'ensuit que
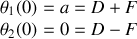
ce qui donne
 ,
,
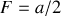 . Pour les vitesses angulaires on a:
. Pour les vitesses angulaires on a:
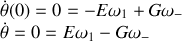
soit
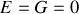 .
.
Il s'ensuit que pour
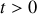 :
:
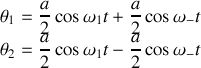
Les 2 modes normaux sont excités simultanément. On constate en réécrivant ces équations que les pendules effectuent des battements
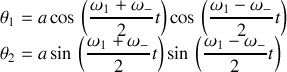
On distingue dans ces 2 solutions la pulsation moyenne
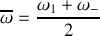 et la pulsation de battement
et la pulsation de battement
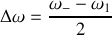 qui est la pulsation de battement entre les 2 ondes. On rappelle à ce stade que
qui est la pulsation de battement entre les 2 ondes. On rappelle à ce stade que
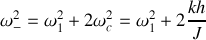
Conseil :
Pour observer de beaux battements il faut donc que

Il est clair que cela se produit si
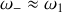 ce qui correspond à un couplage faible. Il faut donc pour bien observer les battements mettre le ressort
ce qui correspond à un couplage faible. Il faut donc pour bien observer les battements mettre le ressort
 à une distance
à une distance
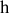 pas trop éloignée de
pas trop éloignée de
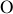 de façon à réduire l'influence du couplage.
de façon à réduire l'influence du couplage.



