Attention :
Pour un système de 2 oscillateurs couplés, il existe 2 modes normaux de vibration pour lesquels tous les oscillateurs vibrent à la même fréquence et ont des amplitudes de vibration fixées.
Remarque :
Si les conditions initiales du mouvement
Correspondent aux modes normaux alors les oscillateurs continueront à osciller selon ces modes normaux
Ne correspondent pas aux modes normaux alors on observe des déplacements non-harmoniques de chaque oscillateur.
Nous allons rechercher des solutions de même pulsation
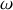en posant:
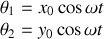
Il s'ensuit que
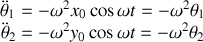
ce qui substitué dans les équations différentielles conduit à:
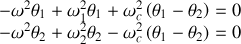
Ces deux équations se réécrivent
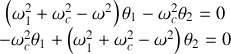
En introduisant
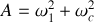et
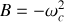, ces équations s'écrivent
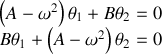
Nous avons donc 2 équations simultanées en
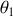et
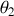qui imposent :
Soit
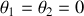(pas de déplacement)
Soit de choisir
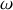pour que ces 2 équations soient identiques
Si tel est le cas alors on détermine le rapport
:
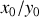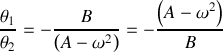
ce qui conduit à
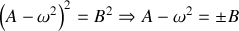
Il s'ensuit que le système peut osciller selon deux pulsations particulières données par :
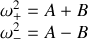
La première solution
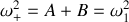n'est rien d'autre que la pulsation propre du pendule pesant non couplé.
La seconde solution
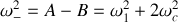dépend du couplage entre les deux oscillateurs.
Remarque :
Les deux pulsations ainsi trouvées constituent les modes normaux de vibration des 2 oscillateurs couplés.
Fondamental :
La connaissance des modes normaux nous permet de remonter aux amplitudes
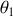et
.
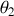Pour la premières valeur de
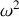on obtient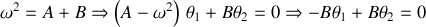
soit
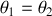
Les deux pendules oscillent alors en phase ; on parlera du mode symétrique .
Pour la seconde valeur de
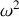on obtient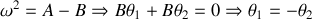
Les deux pendules oscillent alors en opposition de phase ; on parlera du mode antisymétrique .
