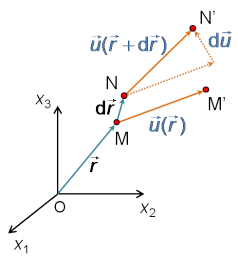
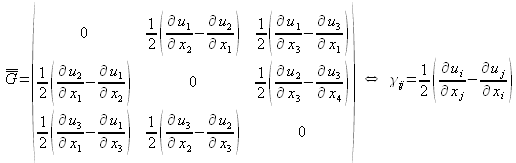Au sein d'un solide sollicité mécaniquement, considérons un point qui se déplace en et un point , voisin de , qui se déplace en (figure 14).

On a donc :

Le déplacement du point N en N', , peut alors se formuler en fonction du déplacement du point M, , et d'un accroissement de déplacement, , caractérisant le fait que chaque point du solide est susceptible de subir un déplacement différent (à l'origine de la déformation) :

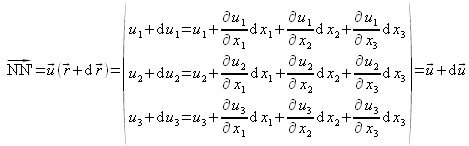
Par identification, on peut formuler l'accroissement de déplacement comme :

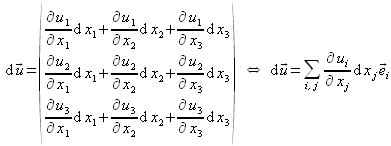
ce même résultat pouvant s'obtenir en introduisant un tenseur :

où est appelé « tenseur des déformations ».

On pourra alors distinguer deux grands types de contribution à la déformation en décomposant ce tenseur comme la somme d'un tenseur symétrique et d'un tenseur antisymétrique : où :

étant le transposé de :

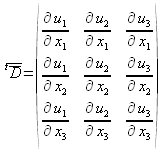
On a ainsi défini le « tenseur des déformations pures » :

et le « tenseur des rotations pures » :