La genèse de la théorie de la mécanique quantique et les différentes contributions qui la constituent ont été accompagnées d'un foisonnement d'idées philosophiques tant les nouveaux concepts bousculent les méthodologies et approches de la physique classique. C'est ainsi que le principe d'incertitude de Heisenberg, énoncé en 1927, a fait l'objet de discussions fécondes et des articles très pertinents sont édités jusqu'à nos jours. Même la référence à la sémantique de la contribution de Heisenberg a été discutée et se trouve qualifié et justifiée par les termes de « principe d'indétermination »
, « théorème de Heisenberg »
ou plus fréquemment maintenant d' « Inégalités de Heisenberg »
. Il convient de souligner que ces inégalités se démontrent grâce au formalisme mathématique de la mécanique quantique développé par les fondateurs de cette théorie (Heisenberg, Dirac, ..) et de ce point de vue l'appellation de « Théorème »
se justifie.
Cependant, l'idée première et simple de cette contribution est que, dans le cadre de la mécanique quantique (action caractéristique ~
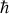 ), tout système physique se caractérise par des grandeurs physiques et la mesure simultanée de certaines d'entre elles ne peut se faire avec une précision arbitraire. En particulier, la position et l'impulsion associée dans la même direction ne peuvent être mesurées simultanément avec une précision en dessous de
), tout système physique se caractérise par des grandeurs physiques et la mesure simultanée de certaines d'entre elles ne peut se faire avec une précision arbitraire. En particulier, la position et l'impulsion associée dans la même direction ne peuvent être mesurées simultanément avec une précision en dessous de
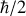 . Ceci nous ramène encore à souligner l'importance de la constante de Planck qui constitue une référence à la précision de la mesure en mécanique quantique comme elle l'est pour justifier la nécessité de la mécanique quantique pour traiter le mouvement selon la grandeur de l'action caractéristique du système par rapport à
. Ceci nous ramène encore à souligner l'importance de la constante de Planck qui constitue une référence à la précision de la mesure en mécanique quantique comme elle l'est pour justifier la nécessité de la mécanique quantique pour traiter le mouvement selon la grandeur de l'action caractéristique du système par rapport à
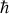 .
.
La notion de la mesure
En physique classique, pour des objets macroscopiques, on peut effectuer des mesures aussi précises que l'on veut à condition que l'expérimentateur et l'appareil aussi parfaits que possible. La mesure simultanée de deux grandeurs (exemple : position et impulsion) ne souffre d'aucune limitation particulière telle qu'une erreur intrinsèque incontournable du fait de la simultanéité de la mesure. Une autre formulation de ce constat serait de dire que l'ordre des mesures effectuées dans les mêmes conditions sur des grandeurs telles que la position et l'impulsion d'un système n'influe aucunement sur la précision des mesures.
En physique quantique, l'opération de la mesure s'effectue selon le même procédé (expérimentateur + appareil de mesure). Or la mesure perturbe le système et de ce fait la mesure simultanée de deux grandeurs conjuguées (exemple : position et impulsion) est assujettie à une limite inférieure pour l'erreur commise lors de cette mesure. Les inégalités de Heisenberg, décrites ci-dessous, précisent la limite inférieure liée aux incertitudes des mesures simultanées de certaines grandeurs physiques.
Processus de la mesure
En mécanique quantique, la mesure d'une grandeur physique G sur un système physique « conditionné »
dans un état donné, fournit comme résultat une valeur
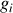 . Or, suite à cette opération, l'état du système a été perturbé et il convient de
. Or, suite à cette opération, l'état du système a été perturbé et il convient de « reconditionner »
le système avant de refaire une seconde mesure de la même grandeur. La répartition de cette procédure un certain nombre de fois (N) permet de déduire la valeur moyenne de grandeur physique :
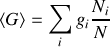
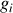 étant une valeur obtenue
étant une valeur obtenue
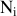 fois durant les N mesures effectuées.
fois durant les N mesures effectuées.
Pour caractériser la dispersion des résultats des mesures autour de la valeur moyenne, on introduit l'écart quadratique moyen définit par la relation suivante :
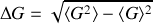
et on assimile la grandeur
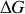 à l'incertitude commise sur la mesure de la grandeur physique G.
à l'incertitude commise sur la mesure de la grandeur physique G.
Inégalités de Heisenberg : Position-Impulsion
On considère comme système physique un corpuscule matériel en évolution dans l'espace selon un repère Oxyz où la position et l'impulsion sont représentées respectivement par
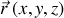 et
et
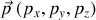 . Les inégalités de Heisenberg s'expriment par :
. Les inégalités de Heisenberg s'expriment par :
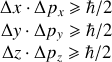
Contenu physique de la relation d'incertitude de Heisenberg
La mesure simultanée de la position et de l'impulsion de la particule ne peut se faire avec une précision arbitraire. Il existe une limite inférieure qui correspond à une incertitude intrinsèque indépendamment de la précision de l'appareil ou du soin avec lequel l'opération de mesure a été effectuée. Les inégalités sont valables uniquement pour les variables conjuguées (
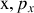 ), (
), (
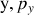 ) ou (
) ou (
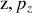 ). Ainsi, une grande précision sur l'évaluation d'une grandeur entraîne une plus grande erreur sur sa variable conjuguée. L'exemple discuté ci-dessous illustre l'inégalité de Heisenberg (position-impulsion)
). Ainsi, une grande précision sur l'évaluation d'une grandeur entraîne une plus grande erreur sur sa variable conjuguée. L'exemple discuté ci-dessous illustre l'inégalité de Heisenberg (position-impulsion)
Exemple : Mesure de la position d'une particule
On considère un électron en mouvement selon un axe Ox avec une impulsion
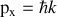 en accord avec l'hypothèse de L. De Broglie. On souhaite déterminer sa position sur l'axe Oy. Pour cela on interpose un écran avec un diaphragme de dimension d selon Oy. Si l'électron franchit le diaphragme, on aura localisé sa position avec une incertitude
en accord avec l'hypothèse de L. De Broglie. On souhaite déterminer sa position sur l'axe Oy. Pour cela on interpose un écran avec un diaphragme de dimension d selon Oy. Si l'électron franchit le diaphragme, on aura localisé sa position avec une incertitude
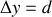 . Or l'onde de de Broglie associé à l'électron va être diffracté par le diaphragme. De façon analogue au phénomène de diffraction d'une onde lumineuse par un diaphragme de dimension comparable à la longueur d'onde du rayonnement (en dehors de la limite de l'optique géométrique), l'ouverture du faisceau est égale à :
. Or l'onde de de Broglie associé à l'électron va être diffracté par le diaphragme. De façon analogue au phénomène de diffraction d'une onde lumineuse par un diaphragme de dimension comparable à la longueur d'onde du rayonnement (en dehors de la limite de l'optique géométrique), l'ouverture du faisceau est égale à :
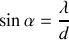
L'impulsion de l'électron dans la direction Oy va être non nulle et donnée par :
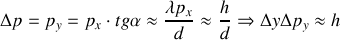
On retrouve ainsi l'ordre de grandeur des incertitudes en accord avec l'inégalité de Heisenberg
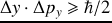
Il convient de noter que le produit position x impulsion possède la dimension d'une action. Or, l'action caractéristique relative à un système dont l'analyse du mouvement repose sur la mécanique quantique, est de l'ordre de
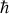 qui constitue l'action élémentaire. Les relations de Heisenberg expriment que lors d'une mesure, l'action ne peut être en dessous de
qui constitue l'action élémentaire. Les relations de Heisenberg expriment que lors d'une mesure, l'action ne peut être en dessous de
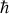 .
.
Inégalité de Heisenberg Temps-Energie
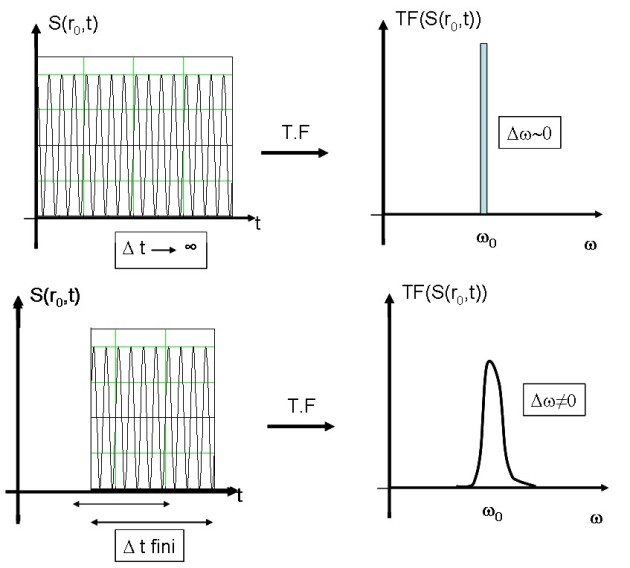
Les phénomènes ondulatoires concernent tout aussi bien un rayonnement que des corpuscules matériels selon L.de Broglie. Or, une onde représentant un rayonnement et utilisée dans sa version idéale d'onde plane, possède une extension infinie aussi bien spatiale que temporelle. Pour une telle onde, la transformée de Fourrier qui donne le spectre en vecteurs d'onde ou pulsation consiste en une distribution de Dirac. Ceci correspond à une absence de dispersion sur la valeur de la pulsation et donc
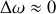 (Figure 8).
(Figure 8).
Si on utilise une onde tronquée dont la durée temporelle
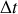 est finie, le spectre en pulsation présente une dispersion de largeur finie
est finie, le spectre en pulsation présente une dispersion de largeur finie
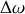 .
.
Ainsi, la durée temporelle de l'onde et la dispersion de sa pulsation varient en sens inverse et le traitement mathématique de la transformée de Fourier établit une relation du type :
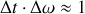
Si on tient compte de la relation d'un quantum d'énergie
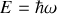 , on en déduit :
, on en déduit :
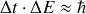
Cette relation est fondamentale pour le rayonnement car elle exprime qu'un rayonnement purement monochromatique n'existe pas et qu'il existe nécessairement une largeur spectrale finie. Or, le rayonnement étant issu de désexcitation d'atomes, on en déduit que les niveaux d'énergie atomiques sont entachés d'une certaine dispersion.
D'après la dualité onde-corpuscule pour des corpuscules matériels, la même analyse effectuée ci-dessus s'applique à des ondes de matières. Dans ce cas, le système (corpuscule matériel) possède une dispersion en énergie inversement proportionnelle à un temps caractéristique de son évolution. Cette situation sera revue lors de la description de l'évolution d'un système par les outils théoriques de la mécanique quantique.