Pour simplifier, plaçons nous d'abord dans le vide. Les équations de Maxwell deviennent alors en l'absence de charges ou de courants
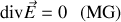
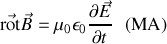
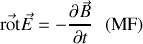
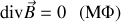
On voit que les équations de Maxwell-Ampère et de Maxwell-Faraday sont mutuellement liées. Prenons par exemple le rotationnel de l'équation de Maxwell-Ampère : on obtient
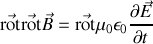
or
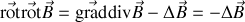
car la divergence de
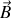est toujours nulle.
Il vient donc
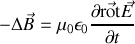
en mélangeant avec l'équation de Maxwell-Faraday
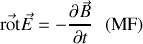
il apparaît
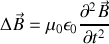
ou encore
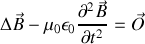
Nous allons voir dans le paragraphe suivant que cette équation est une équation d'onde pour le champ électromagnétique.
En attendant, réalisons l'application numérique approximative
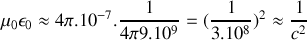
avec
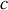célérité de la lumière. Nous comprenons mieux la surprise de Maxwell arrivant à ce résultat et expliquant ainsi par l'introduction du courant de déplacement, permettant le couplage des équations, la nature électromagnétique de la lumière, et prévoyant l'existence d'ondes électromagnétiques de toute fréquence.
Nous pouvons répéter le raisonnement pour le champ électrique en prenant le rotationnel de l'équation de Maxwell-Faraday
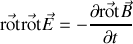
De nouveau
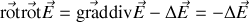
car la divergence de
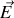est nulle dans le vide par Maxwell-Gauss.
De même Maxwell-Ampère dans le vide donne
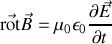
et finalement
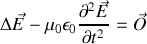
soit exactement la même équation que pour le champ magnétique et les mêmes remarques. Nous allons voir que les ondes électromagnétiques ont simultanément une composante électrique et magnétique.
