Tout d'abord, envisageons en général l'équation aux dérivées partielles dite équation d'onde de d'Alembert (établie historiquement pour une corde vibrante du type corde de guitare)

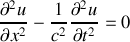
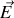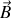où u correspondra par exemple à une des composantes cartésiennes de ou de . Remarquons d'abord que dans cette équation 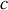a bien les dimensions d'une vitesse. Introduisons deux variables 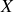et 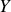telles que

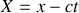
et

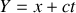
alors réciproquement

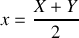
et

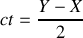
par conséquent

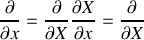
par la règle des dérivées de fonctions composées exprimées comme usuellement en physique ; la même formule peut être exprimée pour 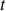et il vient

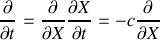
On peut exprimer les mêmes relations pour .

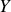Finalement l'équation d'onde

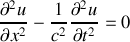
devient

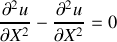
par conséquent toute fonction 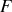de 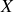est solution de l'équation d'onde, de même que toute fonction 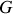de 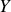. Par superposition nous pouvons donc écrire

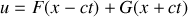
Remarquons que la première partie 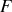correspond à une propagation sans déformation de la forme de 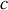à constant (donc à 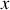croissant pour 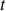croissant) donc à la célérité 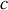. On fait la différence entre la "célérité" de l'onde (correspondant grosso modo à sa vitesse de propagation, comme il peut être démontré dans un cours plus avancé) et la vitesse éventuelle d'un élément du milieu : charge par exemple, ou particules d'air en acoustique.

Figure 1 – Propagation spatio-temporelle des deux types de solution à l'équation d'onde

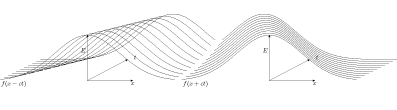
Réciproquement 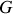correspond à une propagation de l'onde vers les 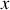décroissants pour 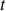croissant ("de droite à gauche" avec les conventions usuelles).

Si les deux formes 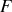et 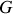sont identiques on peut avoir superposition et obtenir des "ondes stationnaires" (dans une cavité par exemple) avec des maxima dont la position est indépendante du temps. Nous y reviendrons.

On peut pour le moment supposer par exemple .

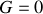Dans ce cas 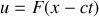. On peut envisager un grand nombre de formes pour 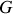mais la plus courante correspond à une décomposition en fréquences spatiales ou temporelles de 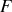(série ou transformée de Fourier). Ainsi si nous posons

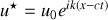
en notations complexes 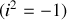correspondant à

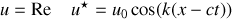
si 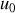est réel on peut vérifier aisément que l'on a une solution.

Réciproquement

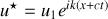
correspondrait à la partie 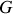de la solution.

Remarquons que si 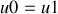alors

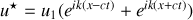
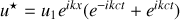
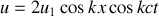
par les formules de Moivre ou d'Euler et dans ce cas on a bien une onde stationnaire qui ne se propage pas : la partie spatiale est constante.