Choisissons par exemple

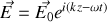
avec

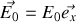
l'équation d'onde étant

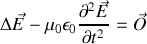
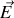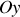On peut aisément vérifier que les projections de sur et 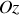étant nulles l'équation d'onde est satisfaite, et sur 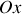on obtient bien une solution si 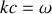avec .

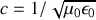Nous avons donc une solution (parmi d'autres possibles, n'oublions pas que comme l'équation est linéaire le principe de superposition s'applique) à l'équation d'onde.

Calculons dans ce cas, par l'équation de Maxwell-Faraday, le champ magnétique correspondant.

Comme

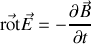
et

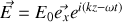
nous obtenons en prenant garde au fait que 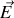est suivant 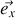mais dépend de 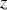et donnera une seule composante non nulle dans le rotationnel

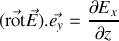
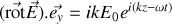
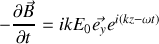
après intégration temporelle en éliminant les signes et à une constante près

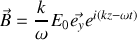
Manifestement 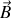ayant la même forme que 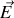obéit également à l'équation de propagation. Remarquons cependant que comme 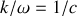la composante magnétique du champ est bien inférieure (en unités SI...) à la composante électrique ; sauf dans des dispositifs spécifiques (cadre à grand nombre de tours) on détectera donc plutôt la composante 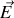du champ électromagnétique.

Figure 2 – Cadre permettant de trouver la direction d'un signal radio (radiogoniométrie) en détectant sa composante magnétique

Si nous introduisons le vecteur 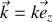, remarquons que 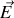, , 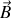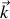forment un trièdre direct et que 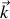est dans le sens de propagation de l'onde. On l'appellera vecteur d'onde pour l'onde étudiée, caractérisée ici par sa nature plane : en effet à un instant donné les lieux d'égale perturbation électrique ou magnétique sont des plans dans l'espace, perpendiculaires à la direction de propagation .

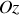Il est à noter que nous aurions pu orienter différemment les axes mais que le résultat aurait été le même. De façon générale, sans particulariser le repère cartésien, nous pouvons écrire pour l'onde

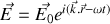
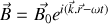
avec 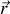vecteur position dans un système de coordonnées et un repère arbitraire. Notons bien l'homogénéité vectorielle de cette formule.

Figure 3 – Structure d'onde plane progressive monochromatique polarisée rectilignement

Par ailleurs, on peut résumer les relations précédentes (Maxwell-Faraday) en remarquant qu'on peut exprimer simplement l'opérateur nabla dans le cas de l'onde plane progressive vers les 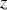croissants par exemple puisque la dérivée spatiale se réduit à une multiplication par 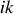et l'intégration temporelle à une division par :

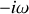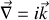
Ainsi

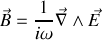
en tenant compte du signe de la loi de Lenz

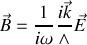
et

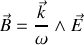
ce qui résume les résultats obtenus précédemment pour une onde plane indépendamment du système de coordonnées.