Considérons maintenant une autre forme pour la solution.

Si nous supposons une symétrie sphérique du problème l'équation d'onde, par exemple pour le champ électrique

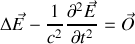
se résume vu l'expression du Laplacien en sphériques à

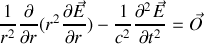
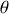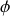les autres termes étant supposés nuls (pas de dépendance des angles polaires et ) . Considérons arbitrairement que 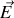est de la forme

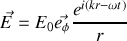
(nous verrons plus tard que cette forme correspond à longue distance à l'onde émise par un dipôle oscillant) alors l'expression de l'équation d'onde en sphériques donne bien 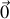après une algèbre un peu longue, en employant deux fois la formule de la dérivée d'un produit par exemple.

Nous avons donc bien une solution possible à l'équation d'onde dans ce cas.

Si par l'équation de Maxwell-Faraday

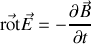
nous calculons le champ magnétique correspondant, comme en sphériques l'opérateur rotationnel vaut pour la coordonnée

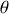
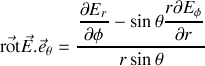
et sera nul ici pour les autres coordonnées donc

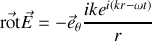
et après intégration temporelle

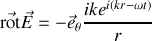
Remarquons encore une fois que 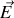, , 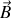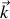forment un trièdre direct si nous prenons 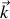suivant la direction de propagation 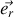avec 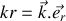. Localement on peut même définir une forme d'onde plane ; ainsi, la lumière émise par le soleil est-elle à symétrie sphérique, et s'atténue en carré de la distance comme nous le verrons dans le paragraphe suivant sur l'énergie et le vecteur de Poynting, mais arrive localement sur Terre sous forme d'une onde plane avec une très bonne approximation.