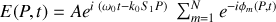Nous étendons le calcul des interférences à deux ondes à celui d'ondes multiples qui se superposent. Ceci fait appel à une structure périodique connue sous le nom de réseau représenté sur la figure 14. Un tel dispositif est constitué de 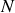ouvertures périodiquement espacées de 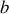. Nous supposons qu'il est éclairé par une onde plane monochromatique.

Figure 14 : Représentation schématique d'un réseau constitué de bandes transparentes de largeur a séparées par des bandes sombres. La périodicité du réseau est notée b

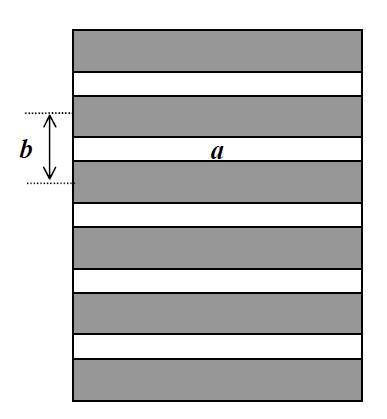
On définit le nombre de traits 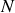du réseau et le nombre de traits par millimètre 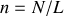. Les réseaux classiques vont de 100 traits au millimètre à 1600 traits par millimètre pour les plus performants.

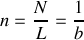
Ces 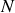ouvertures diffractent la lumière si bien qu'un point 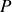très éloigné du réseau peut recevoir la superposition de 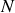ondes issues des 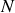ouvertures. Lorsque le point d'observation est très éloigné, ces ondes sont considérées comme planes et l'on fait l'hypothèse qu'elles ont toutes le même vecteur d'onde propagation 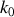. Si l'on regarde dans une direction de diffraction 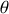, cela signifie que les ondes issues de chaque fente sont déphasées l'une par rapport à l'autre (voir Figure 15).

Figure 15 : Transformation d'une onde plane en une onde sphérique lors de son passage au travers d'un réseau plan

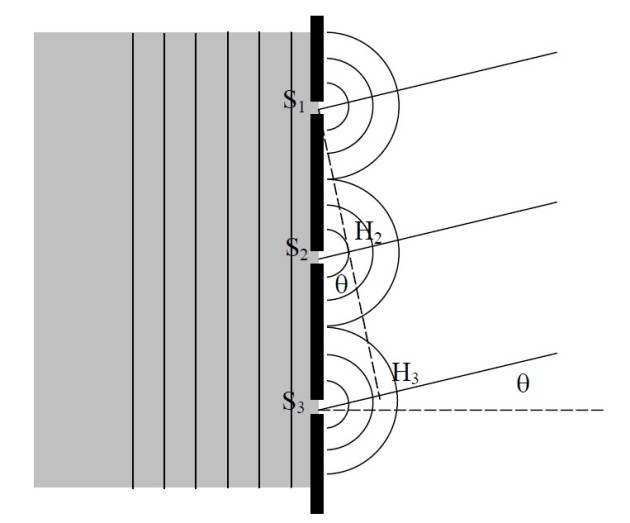
Ainsi l'onde qui émerge de la fente 2 devra pour être dans le même état vibratoire que celui de la fente 1 parcourir la distance supplémentaire 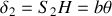. Il en résulte que ces deux ondes sont déphasées de 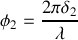. La périodicité du réseau de fentes fait que la différence de marche entre l'onde issue de la fente 1 et celle issue de la fente 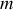augmente linéairement avec 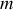. Pour la fente numéro 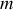, la différence de marche avec l'onde issue de la fente 1 est donc :

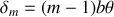
Si l'on prend l'origine des phases sur la fente 1, l'amplitude du champ électrique en 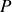est donnée par :

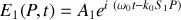
Les ondes émises par les fentes d'ordre supérieur sont en avance de phase par rapport à l'onde émise par la fente 1 et le champ électrique émis par la fente 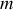s'écrit donc :

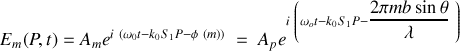
Nous faisons l'hypothèse que l'onde issue de l'ouverture du haut permet de définir la référence des phases et que les ondes issues des ouvertures successives sont déphasées par rapport à cette onde de référence (voir figure). Le champ en 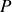est donc obtenu en sommant les champs issus de toutes les ouvertures soit :

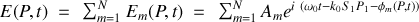
Comme toutes les ouvertures sont identiques les amplitudes des champs issus de ces ouvertures sont égales et