Un observateur regardant à travers un réseau dans la direction
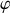 recevra donc une onde dont l'amplitude sera la somme des amplitudes de chaque onde émise par chaque fente affectées d'un terme de phase qui traduit la différence de marche existant entre ces ondes. L'amplitude totale est donnée par :
recevra donc une onde dont l'amplitude sera la somme des amplitudes de chaque onde émise par chaque fente affectées d'un terme de phase qui traduit la différence de marche existant entre ces ondes. L'amplitude totale est donnée par :
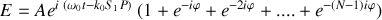
ce qui peut se réécrire sous la forme suivante :
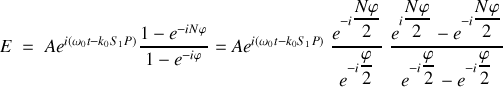
Cette relation peut se transformer en :
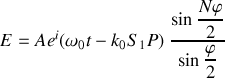
et l'intensité s'écrit :
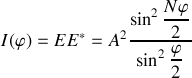
La figure d'interférence est caractérisée par :
des maxima principaux d'amplitude proportionnelle à
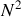
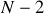 maxima secondaires de très faible amplitude
maxima secondaires de très faible amplitude
 minima nuls
minima nuls ou
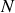 représente le nombre de fentes (ou de traits) illuminées par le faisceau incident.
représente le nombre de fentes (ou de traits) illuminées par le faisceau incident.
La position des maxima principaux est obtenue en annulant la valeur des deux sinus ce qui correspond à la condition d'annulation du sinus qui se trouve au dénominateur c'est à dire :
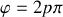
La position des minima est obtenue en annulant le sinus qui se trouve au numérateur sans annuler celui qui est au dénominateur (puisque quand les deux s'annulent en même temps on obtient un maximum principal) soit à chaque fois que :
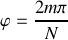
La position des maxima secondaires est obtenue en écrivant que le sinus du numérateur vaut 1 soit :
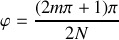
Cette condition n'est vérifiée qu'entre les minima ce qui impose d'éliminer deux valeurs à savoir la valeur correspondant à
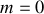 et celle correspondant à
et celle correspondant à
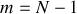 qui conduisent à des maxima secondaires situés entre les maxima principaux et le premier (respectivement dernier) minimum nul. En toute rigueur la position des maxim secondaires est obtenue en annulant la dérivée de l'intensité ce qui conduit à la relation suivante :
qui conduisent à des maxima secondaires situés entre les maxima principaux et le premier (respectivement dernier) minimum nul. En toute rigueur la position des maxim secondaires est obtenue en annulant la dérivée de l'intensité ce qui conduit à la relation suivante :
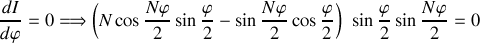
soit
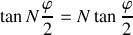
Cette équation est une équation transcendantale en
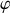 et ne peut être résolue que numériquement. Nous donnons un exemple de résolution graphique de cette relation sur la figure 16 dans le cas où
et ne peut être résolue que numériquement. Nous donnons un exemple de résolution graphique de cette relation sur la figure 16 dans le cas où
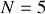 .
.
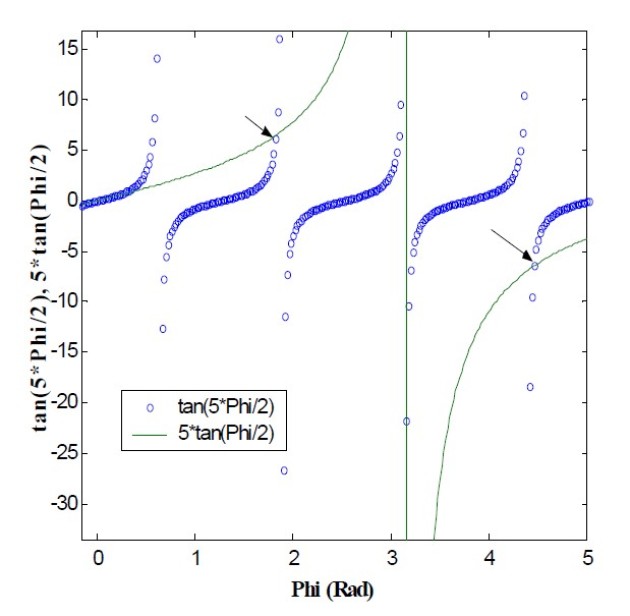
Nous observons qu'il existe en dehors de 0 et de
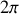 , 2 zéros (marqués par les flèches sur la figure 16) localisés en
, 2 zéros (marqués par les flèches sur la figure 16) localisés en
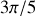 , et
, et
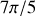 ce qui correspond à la présence dans la courbe d'intensité de
ce qui correspond à la présence dans la courbe d'intensité de
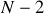 maxima secondaires.
maxima secondaires.
La figure 17 correspond à l'intensité calculée d'une figure d'interférences à 5 fentes.
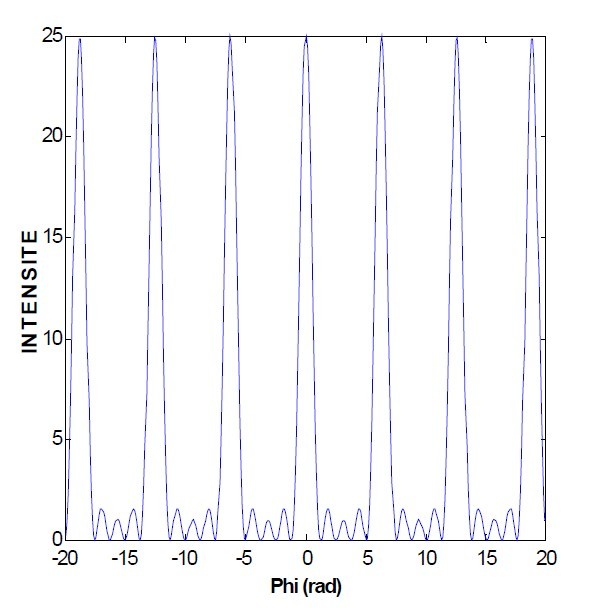
On voit immédiatement sur la figure d'interférences que la lumière issue d'un réseau est constituée de pics très intenses à chaque fois que le déphasage entre les ondes issues de chaque fente est un multiple de
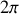 . L'effet est d'autant plus intense qu'il y a plus de traits éclairés sur le réseau puisque l'intensité est proportionnelle à
. L'effet est d'autant plus intense qu'il y a plus de traits éclairés sur le réseau puisque l'intensité est proportionnelle à
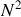 .
.
Remarque :
Si le nombre de traits par mm augmente cela signifie que le réseau est constitué d'ouvertures de plus en plus fines ce qui nuit à la quantité de lumière qui traverse le réseau. Le réseau devient de moins en moins lumineux car l'intensité
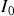 de l'onde émergeante décroît avec l'ouverture des fentes.
de l'onde émergeante décroît avec l'ouverture des fentes.
Complément :
Le calcul précédent est simplifié en ce sens qu'il ne tient pas compte de la contribution de la diffraction par chaque fente du réseau et ne prend en compte que la contribution des interférences entre les sources. Si l'on tient compte de la diffraction par chaque fente on peut alors expliquer la perte de luminosité.




