Le pouvoir de résolution d'un réseau est l'aptitude du réseau à séparer deux longueurs d'onde. Il est défini par le critère de Rayleigh qui considère que deux longueurs d'onde
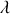 et
et
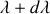 sont séparables si le maximum de l'une (
sont séparables si le maximum de l'une (
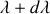 ) est à la position du premier minimum nul de l'autre (
) est à la position du premier minimum nul de l'autre (
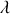 ).
).
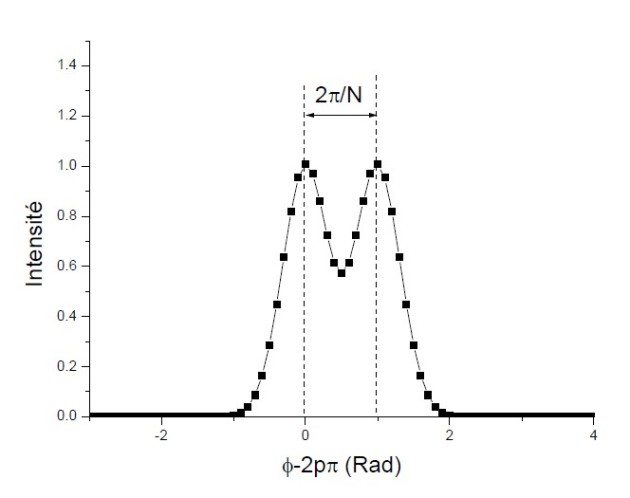
Si l'on se place à l'ordre
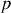 pour la radiation
pour la radiation
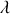 ,la position du premier minimum nul correspond à un déphasage :
,la position du premier minimum nul correspond à un déphasage :
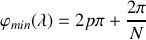
A l'ordre
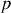 et pour la longueur d'onde
et pour la longueur d'onde
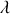 , on observe un maximum si
, on observe un maximum si
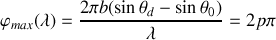
Par différentiation de cette relation on obtient à
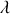 fixé la différentielle de la différence de phase qui donne de combien on doit changer l'angle de diffraction
fixé la différentielle de la différence de phase qui donne de combien on doit changer l'angle de diffraction
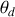 pour changer la phase d'une quantité
pour changer la phase d'une quantité
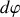
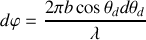
Ce changement de phase est de
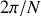 pour passer du maximum au minimum nul immédiatement voisin. Le critère de Rayleigh impose que
pour passer du maximum au minimum nul immédiatement voisin. Le critère de Rayleigh impose que
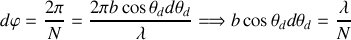
D'autre part si à ordre fixe
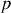 on change la longueur d'onde, la relation fondamentale des réseaux impose que
on change la longueur d'onde, la relation fondamentale des réseaux impose que
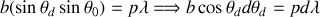
Par identification il s'ensuit que le pouvoir de résolution
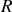 peut s'écrire
peut s'écrire
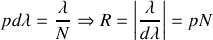
On observe ainsi que le pouvoir de résolution augmente avec l'ordre
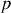 et ne dépend que du nombre
et ne dépend que du nombre
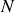 de traits éclairés par la lumière incidente.
de traits éclairés par la lumière incidente.
Pour un réseau contenant
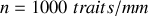 éclairé sur
éclairé sur
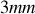 et en se plaçant à l'ordre 1 nous avons :
et en se plaçant à l'ordre 1 nous avons :
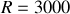
ce qui conduit à séparer pour une longueur d'onde
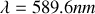 un
un
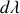 de :
de :
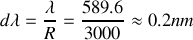
Remarque :
Ce calcul montre ainsi que l'on peut théoriquement séparer le doublet du sodium
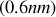 avec un tel réseau à l'ordre 1. Toutefois la résolution d'un réseau dépend beaucoup de la façon dont il est éclairé. Dans les spectrographes à réseau, la largeur de la fente incidente joue un rôle primordial sur le pouvoir séparateur. Cette fente doit être suffisamment fine pour que les radiations soient séparables.
avec un tel réseau à l'ordre 1. Toutefois la résolution d'un réseau dépend beaucoup de la façon dont il est éclairé. Dans les spectrographes à réseau, la largeur de la fente incidente joue un rôle primordial sur le pouvoir séparateur. Cette fente doit être suffisamment fine pour que les radiations soient séparables.




