La déviation du faisceau incident peut être exprimée en fonction des angles d'incidence et d'émergence du faisceau. Elle est donnée par :
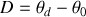
avec
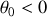
Cette quantité varie en fonction de l'angle d'incidence
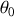et passe par un minimum lorsque :
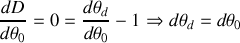
En outre la différentielle de l'équation du réseau donne puisque
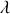est fixe :
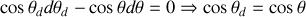
On en déduit que le minimum de déviation est atteint si :
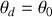ou
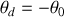
Seule la solution négative est raisonnable puisque l'autre correspond à une déviation nulle ce qui impose :
En reportant cette relation dans l'équation fondamentale, on trouve que la longueur d'onde est reliée au minimum de déviation par :
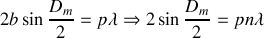
où
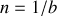désigne le nombre de traits par millimètres du réseau.
Remarque :
Cette relation montre que l'on peut déterminer de façon très précise la longueur d'onde d'une radiation en se plaçant au minimum de déviation. Il suffit pour cela de connaître le nombre
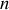de traits par millimètre du réseau et l'ordre
.
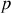