L'équation fondamentale des réseaux s'écrit :
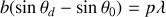
Elle montre que le faisceau incident est dévié sous un angle
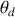qui dépend de :
de l'ordre d'observation
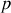
de la longueur d'onde
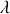
Remarque :
A l'ordre
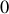il n'y a pas de déviation et la longueur d'onde n'intervient pas. Pour
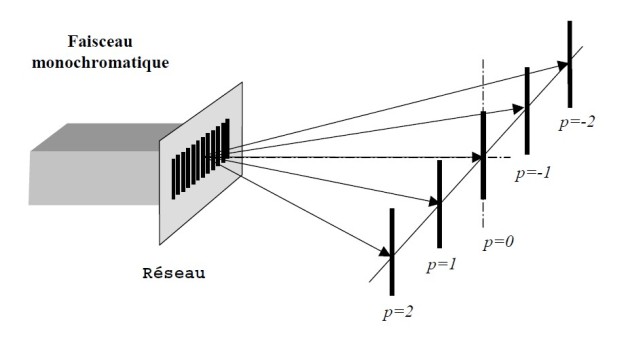
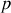différent de zéro, la déviation augmente avec l'ordre d'observation et avec la longueur d'onde. Lorsque le faisceau incident est monochromatique seul l'influence de l'ordre peut être observée. La figure a l'allure suivante :
La figure a l'allure suivante
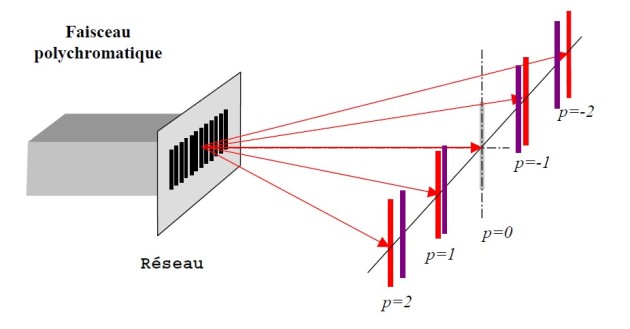
Lorsque la lumière est polychromatique, toutes les longueurs d'onde sont regroupées à l'ordre zéro. Aux ordres supérieurs, les différentes longueurs d'ondes qui composent la lumière sont d'autant plus déviées qu'elles sont élevées et le diagramme à l'allure suivante :
Remarque :
Le phénomène observé est appelé phénomène de dispersion de la lumière polychromatique. Ce phénomène est également visible avec un prisme qui est cependant moins dispersif que le réseau.
L'aptitude du réseau à disperser la lumière est mise à profit pour analyser la nature des sources lumineuses. C'est ainsi que les étoiles ont une composition qui peut déterminée par analyse spectrale à travers un réseau. En effet le spectre de nombreuses sources est un spectre de raies dont les longueurs d'onde sont caractéristiques de l'élément qui constitue la source. Un réseau donne directement la densité spectrale d'une source pour peu que l'axe de déviation soit gradué en longueur d'onde.
Attention :
Le réseau permet donc de déterminer des longueurs d'onde. Il permet en outre de sélectionner dans un spectre certaines longueurs d'onde en utilisant des fentes.
