De ce fait dans la plupart des cas on ne sait pas écrire exactement l'expression du champ électrique associé à l'onde lumineuse et on le modélise par des signaux simples qui cherchent à s'approcher de la réalité. En particulier on évite en général de traiter les ondes lumineuses sous forme de vecteurs et on fait l'approximation des ondes scalaires.

Le signal le plus simple et le plus utilisé à cause de sa simplicité est la cosinusoïde éternelle dont le champ électrique est matérialisé par un signal du type

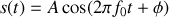
Ce type de signal présuppose que la phase 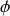et l'amplitude de l'onde 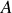sont des constantes. Un tel signal se propage éternellement sans atténuation et est caractérisé par une fréquence 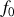particulière. Il correspond à l'image que l'on peut se faire d'une onde plane lumineuse monochromatique de fréquence 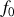ou de longueur d'onde dans le vide 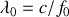d'extension temporelle infinie. Un tel signal est une pure vue de l'esprit et correspond à un signal lumineux parfaitement cohérent dans le temps et dans l'espace. Nous le qualifierons de signal lumineux idéalement cohérent.

D'une façon beaucoup plus générale, le signal lumineux issu d'une source dépendra à la fois du temps et du point 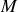où le signal est mesuré. Il sera généralement bien plus compliqué que le signal lumineux idéal. Très peu de sources émettent en effet des signaux purement monochromatiques sous forme d'onde plane. En première approximation les signaux peuvent être représentés par une superposition de signaux monochromatiques présentant une phase et une amplitude dépendant de la fréquence. Les sources usuelles sont donc généralement incohérentes dans le temps (signal non monochromatique) et dans l'espace (source étendue). Nous allons nous limiter dans ce chapitre aux aspects temporel et fréquentiel des signaux lumineux c'est à dire aborder la notion de cohérence temporelle des sources.

Afin de connaître la nature du signal lumineux émis par une source nous allons voir qu'il convient de déterminer la densité spectrale 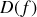du signal c'est à dire la répartition en fréquence de l'intensité lumineuse émise par une source. Pour ce faire on peut analyser la lumière issue de la source au moyen d'un réseau ou d'un prisme dont la fonction sera de décomposer la lumière incidente. Cette technique est difficile à appliquer de façon absolue et on utilise alors la méthode de spectroscopie interférentielle qui permet d'obtenir directement la densité spectrale d'énergie 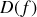contenue dans le signal lumineux. La connaissance de cette fonction permet ensuite de remonter à la nature du signal lumineux émis par la source. Pour comprendre cette démarche il nous faut introduire tout d'abord quelques notions d'analyse des signaux. En effet toute la difficulté de conceptualisation des signaux lumineux repose sur le fait que l'on ne peut pas accéder directement à l'expression du signal 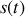ou même à sa transformée de Fourier 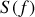dont nous donnons la définition dans le paragraphe suivant.