Définitions
Comme dans de nombreux domaines de la physique (acoustique, traitement du signal...) il est très courant de considérer un signal par sa représentation fréquentielle. Pour cela on fait subir au signal
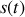 une transformée de Fourier qui fait apparaître les fréquences caractéristiques qu'il contient. On admet alors que si un signal
une transformée de Fourier qui fait apparaître les fréquences caractéristiques qu'il contient. On admet alors que si un signal
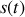 dépendant de la variable
dépendant de la variable
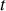 satisfait les conditions de Dirichlet :
satisfait les conditions de Dirichlet :
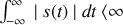 soit
soit
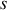 absolument intégrable
absolument intégrable
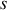 continue par morceaux
continue par morceaux
alors
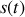 admet une transformée de Fourier définie par :
admet une transformée de Fourier définie par :
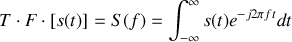
et l'on admet que la transformation inverse existe et est définie par :
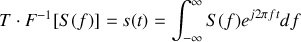
La transformée de Fourier d'un signal temporel peut aussi s'exprimer en fonction de la pulsation
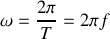
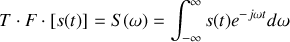
ce qui conduit à l'opération inverse suivante
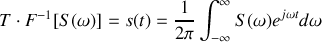
Ainsi que nous l'avions déjà souligné, il se trouve que le signal lumineux
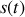 n'est pas directement accessible à l'expérience et il en va de même pour
n'est pas directement accessible à l'expérience et il en va de même pour
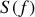 . Les récepteurs lumineux mesurent la moyenne du module au carré de
. Les récepteurs lumineux mesurent la moyenne du module au carré de
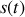 et sont aussi sensibles au module au carré de la transformée de Fourier appelée densité spectrale.
et sont aussi sensibles au module au carré de la transformée de Fourier appelée densité spectrale.
Densité spectrale
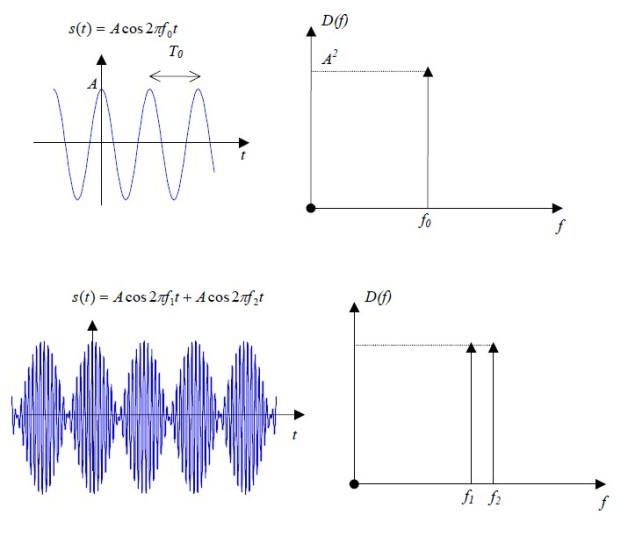
La densité spectrale d'un signal lumineux est obtenue en considérant le module au carré de la transformée de Fourier. Dans le cas d'un signal lumineux, la densité spectrale est aussi appelée la brillance du signal et est définie par
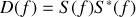
Cette fonction représente la répartition de l'intensité lumineuse en fonction de la fréquence de l'onde (ou de sa longueur d'onde). Un signal idéalement cohérent a une densité spectrale définie par une distribution de Dirac centrée sur la fréquence
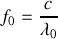 du signal lumineux. Le doublet du sodium présente une densité spectrale composée de deux distributions de Dirac centrées sur chacunes des fréquences
du signal lumineux. Le doublet du sodium présente une densité spectrale composée de deux distributions de Dirac centrées sur chacunes des fréquences
 et
et
 qui composent le doublet.
qui composent le doublet.
On utilise également la densité spectrale normalisée
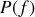 définie par
définie par
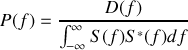
pour représenter la probabilité de trouver une intensité comprise entre
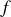 et
et
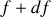 dans le spectre.
dans le spectre.
Les opticiens ont souvent recourt à l'utilisation du nombre d'onde
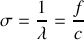
pour matérialiser la fréquence de l'onde et la brillance peut aussi s'exprimer en fonction de ce nombre par
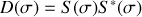
Théorème de Parseval
Ce théorème permet de coupler l'énergie d'un signal dans les domaines temporels et fréquentiels. Pour un signal d'énergie finie nous avons
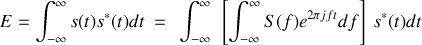
soit encore
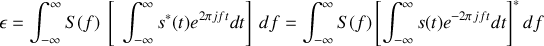
Il s'ensuit que
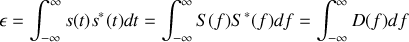
ce qui constitue le théorème de Parseval qui démontre que l'énergie totale contenue dans un signal peut s'exprimer indifféremment dans l'espace temporel ou fréquentiel.
Pour un signal périodique de puissance moyenne finie le théorème de Parseval s'écrit
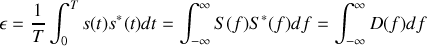
Il s'ensuit que l'intensité mesurée par le détecteur définie par
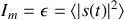
est aussi déterminée par l'intégrale de la densité spectrale sur toutes les fréquences qui composent le spectre de la lumière. Cela signifie en particulier que l'oeil qui observe une source de luminère polychromatique perçoit l'intégrale de la densité spectrale. C'est pour cela que la lumière du soleil nous parâit blanche.




