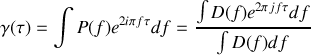Ce théorème est particulièrement important pour tous les processus de diffusion ou de diffraction. Il définit la valeur de la transformée de Fourier de la fonction d'intercorrélation ou d'autocorrélation de deux signaux :
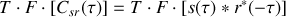
qui par application du théorème de Plancherel sur le produit de convolution conduit à
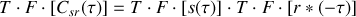
Il faut donc évaluer le dernier terme de cette expression :
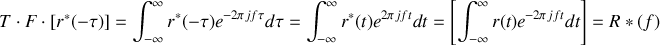
soit
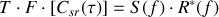
Ceci constitue le théorème de Wiener - Khintchine et montre que dans le cas ou les deux signaux sont identiques alors :
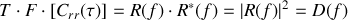
Nous pouvons constater que la transformée de Fourier du la fonction d'autocorrélation du signal
fait apparaître le module au carré du spectre de
. Pour cette raison on dit qu'il s'agit de la densité spectrale d'énergie du signal
.
Théorème : Théorème de Wiener-Khintchine
”La transformée de Fourier de la fonction d'autocorrélation d'un signal est égale à sa densité spectrale en énergie.”
Appliqué à un signal lumineux on voit que sa brillance est obtenue en calculant la transformée de Fourier de la fonction d'autocorrélation du signal. Il s'ensuit que
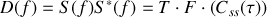
Le corollaire de ce résultat est obtenu en faisant la transformée de Fourier inverse de la brillance ce qui conduit à
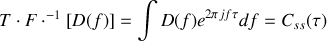
et impose que
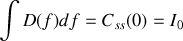
Une bonne connaissance des fonctions de corrélation de quelques signaux usuels permet alors de remonter à l'expression mathématique de
.
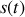En utilisant le théorème de Parseval nous voyons aussi immédiatement que
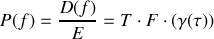
Quelle que soit la source le degré de cohérence est obtenu par transformée de Fourier inverse de la densité spectrale normalisée
