L'équation de désintégration est du type :
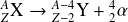
La radioactivité alpha produit seulement deux corps (le noyau fils et la particule alpha). De plus on peut considérer que le noyau père est initialement au repos, donc
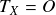et
. En conséquence les équations de conservation s'écrivent :
Conservation de l'énergie :
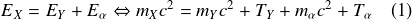
Conservation de la quantité de mouvement :
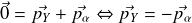
Cette relation implique que les deux corps sont émis dans la même direction mais en sens opposé. De plus, si l'on considère la norme des vecteurs :
Enfin, énergie cinétique et quantité de mouvement sont liées par les relations :
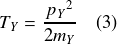et de même
.
On a ainsi à résoudre un système des quatre équations (1), (2), (3) et (4) à quatre inconnues (
,
,
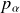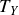et
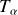). Le système admet donc une solution et une seule.
Fondamental : Conclusion
Ainsi l'énergie cinétique de chacun des deux corps produits (le noyau Y et la particule alpha) est parfaitement déterminée. Pour un nucléide père donné, la désintégration alpha conduit donc à l'émission de particules alpha possédant toutes la même énergie cinétique.
Remarque :
Considérant les relations (3) et (4), comme on a
et
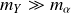, alors il apparaît que
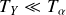. La particule alpha est émise avec une énergie cinétique beaucoup plus grande que le noyau Y.
