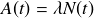Si l'on considère un seul noyau radioactif, il a par unité de temps une probabilité de se désintégrer égale à
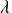(par définition). Par conséquent, pour un échantillon contenant un très grand nombre N de noyaux, le nombre de désintégrations enregistrées par unité de temps, ou autrement dit l'activité, sera :
.
Pourquoi ?
Rappel : Probabilités et statistiques
Pour bien comprendre le lien entre calcul probabiliste et statistique, considérons quelques exemples simples.
Premier exemple :
Imaginons une grande assemblée de 1 000 personnes par exemple. On demande à chacun de jouer à pile ou face avec une pièce de monnaie. Combien de « pile » et de « face » va-t-on comptabiliser ? Intuitivement, on a tendance à dire : approximativement 500 « pile » et 500 « face ». Comment obtient-on ces nombres ? En multipliant la probabilité d'obtenir « pile » (ou « face »), c'est-à-dire 0,5, par le nombre de personnes dans l'assemblée.
Deuxième exemple :
On considère un dé non truqué à six faces, numérotées de 1 à 6. Si on lance le dé une fois, on a une probabilité égale à
d'obtenir par exemple le 6 (ou tout autre chiffre d'ailleurs). Cette probabilité est indépendante du temps écoulé avant le lancer en question : même si vous avez lancé le dé cent fois avant ce lancer particulier, la probabilité d'obtenir le 6 sera toujours de
.Supposons maintenant que vous lanciez le dé mille fois de suite, et que vous enregistriez à chaque lancer le chiffre obtenu. A la fin de cette expérience, combien de fois aurez-vous obtenu le 6 ?
Réponse : approximativement
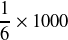soit environ 167 fois (en moyenne). Pour un grand nombre de lancers, vous pouvez ainsi faire un calcul statistique connaissant la probabilité d'obtention du chiffre 6.
Application à la radioactivité :
Pour les lois de la radioactivité, c'est un peu la même chose. Par unité de temps :
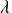est la probabilité pour un noyau de se désintégrer. Pour N noyaux dans un échantillon (N étant très grand), on peut donc prévoir que l'on enregistrera en moyenne
désintégrations. On retrouve ainsi la définition de l'activité.
On peut donc écrire :
|
|---|
Cette relation est vraie quel que soit le temps t considéré.
Ainsi, l'activité est une grandeur proportionnelle au nombre de noyaux radioactifs dans l'échantillon (puisque
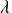est une constante ne dépendant que de la nature du radionucléide considéré). Ceci paraît tout à fait logique : imaginons que l'on ait un échantillon deux fois plus gros, alors son activité sera également deux fois plus grande.
