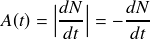On considère la désintégration d'un noyau radioactif X en un noyau fils Y (pouvant être lui-même stable ou bien radioactif). On s'intéresse à l'évolution du nombre de noyaux X dans le temps. On suppose qu'aucune autre réaction nucléaire ne vient produire ce noyau X par ailleurs.
Soit
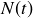le nombre de noyaux radioactifs X dans l'échantillon à l'instant t. Ce nombre N diminue dans le temps : pendant le temps dt, une certaine quantité
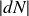de noyaux se désintègre. Par unité de temps, il en disparaît donc une quantité
.
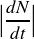Par unité de temps, le nombre de noyaux qui disparaissent est égal (en valeur absolue) au nombre de désintégrations qui se produisent, c'est-à-dire à l'activité. Donc l'activité et le nombre de noyaux sont liés par la relation suivante :
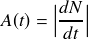
Comme le temps dt considéré ici est très petit, on peut assimiler
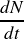à la dérivée de la fonction
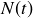. Cette dérivée est négative puisque N diminue dans le temps, c'est pourquoi on a utilisé des valeurs absolues dans les expressions ci-dessus (l'activité est par définition une grandeur toujours positive).
Rappel : Variation, taux de variation, dérivée
La dérivée première
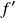d'une fonction
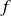de la variable t peut être assimilée à une petite variation relative de la fonction
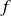autour d'une valeur t donnée. C'est le sens de la définition mathématique de la dérivée :
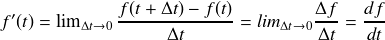
Finalement, on peut donc écrire :
|
|---|
