Question 1
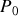 est la pression extérieure qui s'applique au gaz parfait par l'intermédiaire du piston. Elle est la résultante de la pression atmosphérique extérieure et de la pression due au poids du piston :
est la pression extérieure qui s'applique au gaz parfait par l'intermédiaire du piston. Elle est la résultante de la pression atmosphérique extérieure et de la pression due au poids du piston :
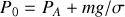
Question 2 : Compression ou détente par ajout ou retrait d'un poids
a) La pression extérieure qui s'applique au gaz parfait par l'intermédiaire du piston augmente de façon discontinue, de la quantité
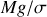 . L'équilibre mécanique initial est rompu et le piston va se déplacer jusqu'à ce qu'il soit rétabli. La transformation du gaz parfait qui en résulte n'est donc pas quasistatique. Par ailleurs elle est adiabatique car le cylindre et le piston sont adiathermes par hypothèse (de toutes façons, la transformation est supposée suffisamment rapide pour que les échanges thermiques n'aient pas le temps de se produire). La transformation est une compression adiabatique irréversible (s'accompagnant d'une augmentation d'entropie de l'Univers).
. L'équilibre mécanique initial est rompu et le piston va se déplacer jusqu'à ce qu'il soit rétabli. La transformation du gaz parfait qui en résulte n'est donc pas quasistatique. Par ailleurs elle est adiabatique car le cylindre et le piston sont adiathermes par hypothèse (de toutes façons, la transformation est supposée suffisamment rapide pour que les échanges thermiques n'aient pas le temps de se produire). La transformation est une compression adiabatique irréversible (s'accompagnant d'une augmentation d'entropie de l'Univers).
b)
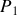 est la résultante de la pression extérieure initiale et de la pression due au poids déposé :
est la résultante de la pression extérieure initiale et de la pression due au poids déposé :
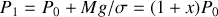 où
où
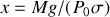
c) La transformation est une adiabatique. Par suite,
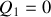 .
.
En revanche, la variation d'entropie est différente de zéro, car la transformation est irréversible. Pour cette adiabatique, on doit même avoir, en vertu du second principe :
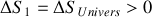 . Par ailleurs la variation de la fonction d'état entropie entre un état initial et un état final ne dépend pas du chemin suivi.
. Par ailleurs la variation de la fonction d'état entropie entre un état initial et un état final ne dépend pas du chemin suivi.
En particulier pour le gaz parfait, on a :
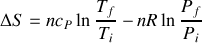 (cf. question 5 de la première partie (Généralités sur le gaz parfait)
(cf. question 5 de la première partie (Généralités sur le gaz parfait)
Par suite :
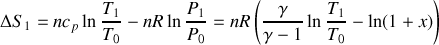
d) La transformation n'étant pas quasi-statique, il faut revenir à la définition générale du travail thermodynamique des forces de pression :
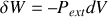 . De plus, au cours de la transformation la pression extérieure reste égale à la constante
. De plus, au cours de la transformation la pression extérieure reste égale à la constante
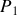 . Par suite :
. Par suite :
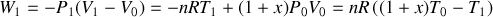
D'autre part d'après le premier principe, la transformation étant adiabatique,
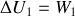 .
.
e) D'après la première loi de Joule, le coefficient
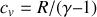 étant constant,
étant constant,
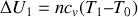 .
.
Par identification avec le résultat de la question précédente, il vient :
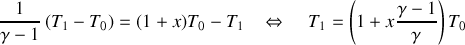
On en déduit immédiatement :
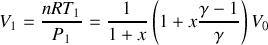
f) Le système étant adiabatique, la variation d'entropie de l'Univers est identique à celle du système. Par suite, la variation d'entropie du système doit être positive (cas irréversible) ou nulle (cas réversible). Comme la transformation étudiée n'est pas quasistatique et est donc nécessairement irréversible, on vérifie que
 :
:
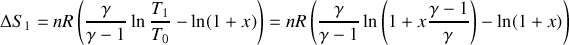
d'où
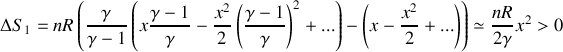
(résultat valable quel que soit le signe de
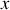 , que la masse soit ajoutée ou retirée ; cela montre également le caractère irréversible de ce type de transformation).
, que la masse soit ajoutée ou retirée ; cela montre également le caractère irréversible de ce type de transformation).
g) Au cours de la transformation précédemment étudiée, le poids de la masse
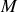 a communiqué au gaz une énergie correspondant à la différence entre son énergie potentielle initiale et son énergie potentielle finale :
a communiqué au gaz une énergie correspondant à la différence entre son énergie potentielle initiale et son énergie potentielle finale :
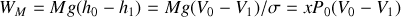 . Si un opérateur retire cette masse, le piston va remonter mais ce n'est pas lui, mais l'opérateur, qui va restituer à la masse M l'énergie potentielle perdue. Le gaz aura donc acquis de l'énergie de façon irréversible.
. Si un opérateur retire cette masse, le piston va remonter mais ce n'est pas lui, mais l'opérateur, qui va restituer à la masse M l'énergie potentielle perdue. Le gaz aura donc acquis de l'énergie de façon irréversible.
Si les frottements sont négligeables (ce qui n'est pas très réaliste), le piston va remonter plus haut que sa position initiale. En effet, la pression sera alors revenue à
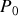 et la température finale
et la température finale
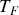 sera plus grande que
sera plus grande que
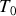 (du fait de l'acquisition de l'énergie). Le volume final
(du fait de l'acquisition de l'énergie). Le volume final
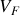 sera donc également plus grand que
sera donc également plus grand que
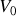 (car
(car
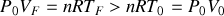 ).
).
N.B. : pour connaître la température finale
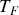 (ce qui n'était pas demandé), il faut également considérer le travail fourni par le piston de la hauteur
(ce qui n'était pas demandé), il faut également considérer le travail fourni par le piston de la hauteur
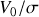 à la hauteur
à la hauteur
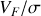 , soit
, soit
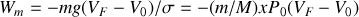 . La variation d'énergie interne entre états initial et final est donc :
. La variation d'énergie interne entre états initial et final est donc :
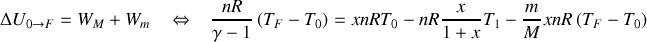
La résolution de cette équation à une inconnue permet d'accéder à la valeur de
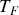 en fonction de
en fonction de
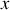 (avec
(avec
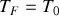 si
si
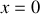 ).
).
Question 3 : Compression par ajout progressif de petits poids
a) Il faut bien évidemment ajouter la même masse
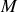 pour aboutir à la même pression finale :
pour aboutir à la même pression finale :
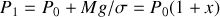
b) Cette fois, la pression extérieure reste à peu près égale à la pression interne à tout instant. La transformation est une succession d'états de quasi-équilibre. C'est une transformation quasistatique. Comme elle reste adiabatique, elle peut même être qualifiée de compression adiabatique réversible de gaz parfait, obéissant en particulier à la loi de Laplace.
c) En utilisant la loi des gaz parfaits, la loi de Laplace peut être écrite indifféremment
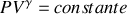 ou
ou
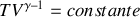 ou
ou
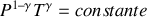 . Par suite :
. Par suite :
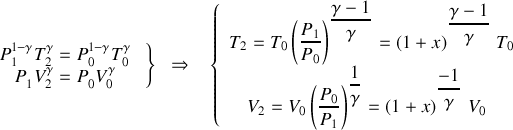
d) La transformation étant adiabatique réversible, on a à la fois
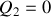 et
et
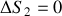 .
.
Par suite,
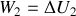 . Soit, en vertu de la 1ère loi de Joule :
. Soit, en vertu de la 1ère loi de Joule :
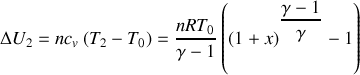
e) Il est loisible d'effectuer un développement limité des expressions de
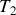 et
et
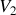 :
:
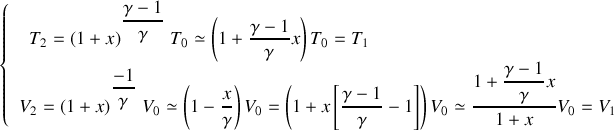
On peut, si
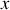 est très petit devant un, identifier
est très petit devant un, identifier
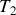 et
et
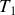 d'une part,
d'une part,
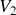 et
et
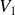 d'autre part. A la limite
d'autre part. A la limite
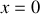 (masse
(masse
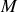 tendant vers zéro) le calcul associé à la transformation irréversible rejoint heureusement celui associé à la transformation réversible.
tendant vers zéro) le calcul associé à la transformation irréversible rejoint heureusement celui associé à la transformation réversible.



