L'énergie cinétique, proportionnelle à la vitesse, permet de décrire "même" une particule libre : c'est l'énergie nécessaire pour vaincre l'inertie de la masse.
Si la particule est immobile ou se déplace avec un mouvement rectiligne uniforme, son énergie cinétique est constante et dépend de sa masse et du module de la vitesse de déplacement.
La constance de la direction et du module de la vitesse
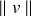est contenue dans une relation en
.
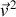En effet :
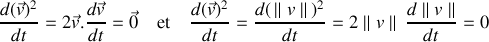
Par définition, la vitesse est tangente à la trajectoire.
Sa dérivée est
soit perpendiculaire à cette trajectoire (produit scalaire nul)
soit nulle (dérivée du module de la vitesse nulle).
Pour la particule libre, cette seconde déduction est vraie, immobilité comprise.
Plus généralement et pour une particule de masse
en déplacement avec une vitesse
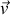, l'énergie cinétique est notée :
.
Elle est positive. (voir le grain 2 sur le formalisme lagrangien)
Fondamental : Généralisation au problème à N corps
L'énergie cinétique est additive.
Pour
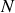particules notées
, de masses
et de vitesses
, l'énergie cinétique totale est :
Elle est toujours positive, globalement proportionnelle à la masse (ou aux masses).
L'énergie cinétique est toujours associée à un effet d'inertie : c'est l'énergie qu'il faut fournir pour déplacer chacune des masses
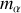, vaincre l'effet passif de chaque masse.
Complément : Un autre mouvement uniforme
A titre d'exercice complémentaire et pour une particule unique, avec les mêmes équations de conservation de l'énergie cinétique (et du carré du vecteur vitesse), la possibilité d'un mouvement plan... à 2 dimensions dans l'espace permet de retrouver un autre mouvement uniforme (et non rectiligne) : celui circulaire.
La variation de l'énergie cinétique, nécessairement produite par une variation de vitesse en mécanique classique, peut être mesurée si la source des variations est identifiée.
C'est le théorème de l'énergie cinétique.
Fondamental : Théorème de l'énergie cinétique
Pendant un déplacement et si la résultante des forces est non nulle, la variation de l'énergie cinétique (
) égale le travail (
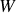) des forces appliquées.
Mathématiquement et pour un déplacement élémentaire entre les états 1 et 2, ce théorème s'écrit :
Le travail est
positif si la force est motrice,
négatif s'il y a opposition au mouvement et pertes en énergie cinétique.
Ces propriétés sont en relation directe avec celles du produit scalaire.
Pus précisément, une interprétation de ce théorème en terme d'efficacité, due à la notion de produit scalaire, est :
Seule la composante de la résultante des forces dans la direction du mouvement contribue à la variation d'énergie cinétique
puisque :
.
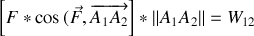Dans le cas particulier de la particule libre, son énergie cinétique est constante.
La résultante des forces appliquées est nulle ou perpendiculaire à la trajectoire (et inefficace) : elle n'y "travaille" pas.
