Dans ce qui suit, l'énergie potentielle de pesanteur qui intervient dans de nombreux exercices est traitée en toute généralité.
L'accent est mis sur le sens choisi de l'axe vertical, source d'erreurs répétées et d'incompréhension.
L'énergie potentielle décrit donc un "état d'énergie" de l'espace.
Cet état est issu du champ local produit par une source (masse ou charge) située à distance.
Cette source étant fixe, l'état d'énergie de l'espace est également fixe quel que soit le référentiel utilisé.
À une constante près. Et seule son écriture peut changer.
Trois exemples suivent dont l'intérêt portera sur leur traitement par les énergies.
Les deux premiers exemples ont un seul degré de liberté : une variable suffit à les décrire.
Dans ce cas, la conservation de l'énergie mécanique totale permet de déduire l'équation différentielle du mouvement.
Le dernier exemple décrit de façon générale un système à 3 degrés de liberté : la seule conservation de l'énergie mécanique totale ne permet pas de conclure même si des pistes sont fournies.
Attention : L'énergie potentielle de pesanteur
Lorsque la force de pesanteur intervient dans le mouvement d'un système, sa direction (axe) et son sens sont définis.
Le choix du sens de l'axe n'a aucune influence sur la force qui s'exerce.
Et donc aucune sur l'énergie potentielle.
En effet : au dessus du niveau de référence choisi pour l'énergie potentielle nulle, celle-ci est positive et en dessous elle est négative.
Explication :
La force de pesanteur est notée :
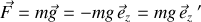
en considérant les deux sens de l'axe vertical.
La force est exprimée respectivement avec un axe orienté vers le haut (
) ou vers le bas (
).
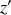Les deux vecteurs unitaires représentant les
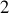orientations de l'axe vertical sont tels que :
.
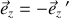Le sol est en
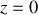. L'énergie potentielle y est nulle.
Tout point de l'espace est caractérisé par sa "hauteur"
si l'axe est orienté vers le haut ou
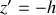s'il est orienté vers le bas.
La hauteur h est positive si l'objet se trouve au dessus du sol, négative sinon.
C'est de fait une valeur algébrique.
L'énergie potentielle en ce point doit avoir la même valeur qu'elle soit déduite de la relation :
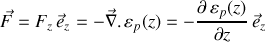
ou de celle -ci :
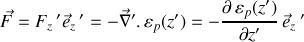
Elle s'écrit sous forme différentielle et dans toutes les notations (c'est la même) :
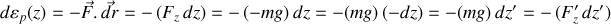
Avec le niveau de référence de l'énergie potentielle choisi en
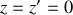(au sol), soit :
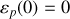, une intégration de l'égalité entre
le sol
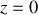pour supprimer la constante, et une hauteur quelconque
(ou
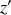selon l'orientation choisie, "haut" ou "bas")
permet de déduire dans le cas général :
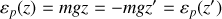
Cette expression acte le concept d'égalité puisque pour le point considéré
et
.
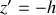Au dessus du sol où elle est nulle, l'énergie potentielle de pesanteur est positive (
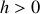), en dessous elle est négative
.
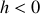Indépendamment de l'orientation de l'axe vertical.
Exemple : 1. Force de rappel à une dimension
Cette situation est souvent représentée par un ressort horizontal de constante de raideur
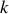auquel est accroché une masse
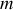(fig. 7).
Le poids de la masse
est alors directement compensé par la réaction du sol
.
La force de rappel du ressort est proportionnelle à la variable
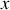représentant l'allongement du ressort par rapport sa longueur à vide
(fig. 7).
Elle est donnée par :
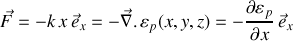
L'énergie potentielle est obtenue à une constante près, nulle dans notre cas,
- 1) par intégration par rapport à la valeur de référence (ressort à vide) et
- 2) puisque les dérivées partielles par rapport aux variables
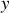et
sont nulles.
L'expression de l'énergie potentielle élastique est :
.
La conservation de l'énergie mécanique totale :
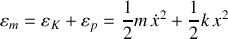
conduit à :
.
Apparaissent deux solutions :
celle triviale (
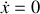) et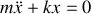 
correspondant à l'application du PFD selon la direction
.
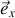Le mouvement obtenu est périodique : harmonique avec une pulsation
.
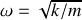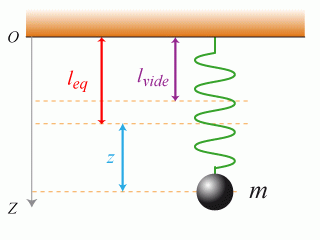
Complément : Et si le ressort était vertical ?
Dans le cas d'un ressort vertical, caractérisé par une oscillation le long de l'axe
, tout ce qui précède est valide moyennant quelques observations. (fig. 8)
Par une simple "bonne pratique expérimentale", chacun sait que la mesure de la période des oscillations passe par deux étapes.
Après avoir accrochée la masse
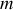, il faut
l'accompagner vers sa position d'équilibre
, différente de la position du ressort à vide
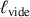, avant de l'en écarter verticalement par une compression ou un allongement du ressort
.
La position d'équilibre,
, se met en place par un allongement constant du ressort autour de laquelle vont se produire les oscillations.
Elle vérifie la condition d'équilibre :
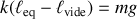, ce qui permet d'annuler l'effet de la pesanteur sur les oscillations.
En effet, si pendant le mouvement, la position de la masse est repérée par
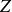, l'allongement du ressort par rapport à sa longueur à vide est
.
Pour une énergie potentielle de pesanteur de référence telle que
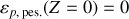, l'énergie mécanique totale du ressort vertical, pesanteur comprise s'écrit :
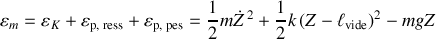
Le repérage par rapport à la position d'équilibre a lieu selon la variable
telle que :
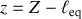ou encore
.
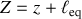Reportée dans l'énergie mécanique, cette expression permet de déduire :
Ou encore, après développement en fonction de la variable du système
,
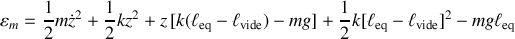
Cette expression met en évidence deux termes constants, les deux derniers.
Le troisième terme s'annule par définition de l'équilibre : ainsi disparaît la pesanteur, annulée par la position d'équilibre.
Ne subsiste donc que l'oscillation pure autour de la position d'équilibre
.
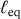L'oscillation
du ressort s'effectue à la pulsation
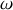précédemment définie.
Complément : Équilibre et oscillations
Tout système physique (1-D) a une position d'équilibre stable,
, si son énergie potentielle présente un minimum autour de cette position.
En effet :
Au voisinage du point d'équilibre (du minimum) l'énergie potentielle se met sous la forme :
.
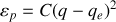La force issue de cette énergie potentielle s'écrit :
Sur un graphique représentant la courbe de l'énergie potentielle et son minimum, le gradient de la courbe caractérise la pente en chacun de ses points :
négative avant le minimum pour
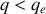et positive pour
.
La force ayant le signe opposé du gradient, elle exercera toujours un rappel vers le point d'équilibre puisqu'elle est toujours dirigée vers le minimum
.
Remarque :
Tous les systèmes mécaniques décrits par une énergie potentielle, réelle ou effective présentant un minimum, et pas forcément symétrique en x, voient des comportements d'abord harmoniques, puis périodiques quand leur énergie initiale augmente : ce sont les états liés ou localisés dans l'espace.
Ainsi les liaisons chimiques présentent une énergie minimale caractérisant la distance minimale de la liaison : une distance d'équilibre entre les charges positive et négative en interaction (voir ci-après et problème à 2 corps).
Une perturbation dans la disposition des charges (par pression mécanique, ou application d'un champ électrique ou électromagnétique par exemple) produit des oscillations du couple de charges, à l'origine d'ondes se propageant dans le milieu environnant et portant l'information sur la perturbation subie.
Dans tout problème à une variable, ou degré de liberté, la conservation de l'énergie mécanique conduit directement à l'équation du mouvement.
C'est également le cas de l'exemple suivant qui a lieu dans le plan (
) mais avec un seule degré de liberté.
Exemple : 2. Glissade sur un igloo.
Le mouvement du point matériel, de masse
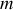, s'effectuant sans frottement, la force de contact
présente en réaction au poids de l'objet est normale à la surface de contact (fig. 9).
Elle n'est cependant pas compensée par le poids.
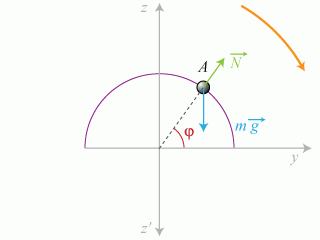
La contribution énergétique de type potentielle à l'énergie mécanique totale est uniquement celle de la pesanteur donnée par :
.
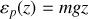La nuance apparaît lorsqu'on veut exprimer l'énergie cinétique.
Le mouvement sur un igloo parfaitement circulaire est décrit avec les coordonnées polaires, soit :
,
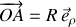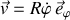, et
.
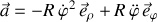ou en coordonnées intrinsèques : l'arc
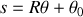avec
.
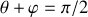L'énergie mécanique totale s'écrit :
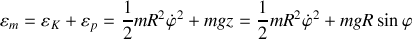
en fonction de la variable du problème.
La variation au cours du temps produit alors :
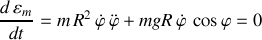
ou encore
Cette équation correspond à celle obtenue avec le PFD selon
.
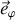Selon
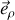, accessible par le formalisme vectoriel du PFD seul, la réaction du support (perpendiculaire à l'igloo) et la composante du poids de l'objet sont associées dans l'expression suivante :
.
La contribution de la force issue de l'accélération (ou force d'inertie) tend à alléger la composante du poids et permet à la réaction du support
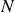de s'annuler et à l'objet de décoller pour une valeur particulière de
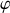, caractérisée par
.
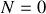Complément :
Dans le cas de la fig. 9, le mouvement du point matériel s'effectue dans les sens opposé à la trigonométrie.
L'axe
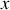est perpendiculaire au plan
de la figure et orienté sortant.
Le vecteur vitesse angulaire s'écrit
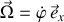, il dirigé selon
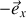puisque
.
Cette exercice peut être traité au moyen de du théorème du moment cinétique : l'équation du second degré pour
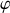peut être ainsi directement obtenue.
Dans ces exemples à un degré de liberté (une inconnue), la conservation de l'énergie suffit à trouver directement l'équation du mouvement (une inconnue → une équation).
Pour 2 degrés de liberté et au delà, une analyse plus complète et plus diversifiée est nécessaire pour déduire les équations du mouvement.
En résumé, autant d'équations sont nécessaires que d'inconnues.
Exemple : 3. Force gravitationnelle ou électrostatique et énergie potentielle
Deux types de forces peuvent être traités en adoptant la notation sphérique suivante pour la force et l'énergie potentielle :
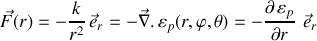
et
où la constante
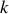peut représenter aussi bien
, l'interaction gravitationnelle entre deux masses
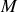et
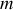, que
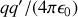, l'interaction électrique entre deux charges.
Sans aucune autre donnée, la symétrie sphérique permet de simplifier l'écriture puisque l'énergie potentielle est indépendante des variables
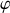et
.
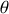En notations standards,
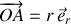et l'élément différentiel s'écrivant
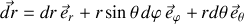, la vitesse prend la forme :
.
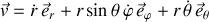L'énergie mécanique totale s'écrit alors :
La dérivée de l'énergie mécanique, en fonction des variables spatiales
,
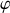et
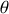s'écrit :
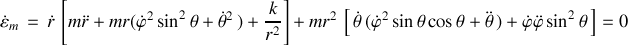
Pour aller au-delà et avoir quelque information sur les directions concernées par chaque terme, les composantes sphériques de l'accélération sont exprimées pour une comparaison.
L'utilisation des dérivées par rapport au temps des vecteurs unitaires devient nécessaire.
Leurs expressions sont données par :
,
.
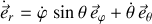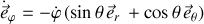
L'accélération en coordonnées sphériques prend alors la forme suivante :
.
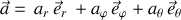où les
composantes de l'accélération sont :
.
.
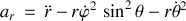Avec trois variables spatiales, la conservation de l'énergie mécanique totale (ou théorème de l'énergie cinétique pour les systèmes conservatifs) conduit à une seule équation.
Mais le premier terme, proportionnel à
, présente des similitudes avec la composante radiale
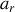de l'accélération.
Ceci suggère de retrancher et d'ajouter des termes qui peuvent conduire à l'apparition des autres composantes de l'accélération.
Ainsi il apparaît que :
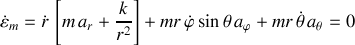
Cette équation apparaît alors sous la forme d'une somme de
termes mettant en jeu chacun une composante de l'accélération.
Intuitivement, UNE solution serait d'annuler chacun des termes.
Mais d'autres solutions peuvent exister.
L'équation du mouvement ne peut donc être obtenue sans données, observations supplémentaires.
Ces données seront présentées plus loin : elles permettront l'annulation effective de chacun des
termes ci-dessus, séparément.
