Le "potentiel" énergétique qui caractérise certaines forces est décrit par leur énergie potentielle.
Cette notion de 'potentiel' peut être associée à un champ représentant des propriétés de l'espace et/ou une action à longue distance.
Une particule - témoin, placée en un point de l'espace, "se chargera d'énergie potentielle", propre au potentiel du lieu : un mouvement en résultera.
Ainsi ces forces sont décrites comme dérivant d'un potentiel ou d'une énergie potentielle.
Définition : L'énergie potentielle
La force
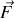dérive d'une énergie potentielle
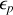si :
la relation
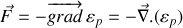
ou encore
la forme différentielle équivalente
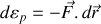
sont vérifiées.
Remarque : 1. L'opérateur "nabla"
Apparaît l'opérateur vectoriel et différentiel "gradient" ou "nabla" noté
.
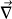Il a 3 composantes spatiales,
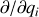où
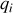est une variable d'espace, dépendant du système de coordonnées utilisées.
Cet opérateur s'applique à une fonction scalaire.
Remarque : 2. Propriétés de l'énergie potentielle.
L'énergie potentielle
ne dépend que des coordonnées spatiales et
est définie à une constante près.
Énergie potentielle et travail
Dans la formulation différentielle de l'énergie potentielle, sa variation est associée au travail élémentaire d'une force via l'expression
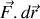dans la formulation différentielle :
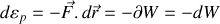
L'intégrabilité du travail sur un parcours donné dépend de la forme de la force : la formulation différentielle de l'énergie potentielle permet d'assurer une continuité des propriétés du potentiel dans l'espace.
Mathématiquement, le travail de la force devient une différentielle totale exacte, donc intégrable : entre les deux points
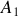et
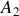d'un déplacement, le travail ne dépend alors que de ses valeurs initiale et finale.
L'utilisation du théorème de l'énergie cinétique permet d'associer énergies cinétique et potentielle dans une nouvelle énergie dénommée énergie mécanique totale.
Elle est représentée par la somme des énergies cinétique et potentielle.
En effet :
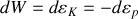ou
.
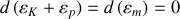Cette expression signe l'existence d'une conservation de la somme de deux termes.
Définition : Énergie mécanique totale et systèmes conservatifs
L'énergie mécanique totale est définie par :
,
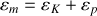une expression valide en tout point de l'espace.
Pour un système conservatif, uniquement soumis à des forces dérivant d'une énergie potentielle, l'énergie mécanique totale est constante dans l'espace et au cours du temps.
Propriétés de l'énergie mécanique totale
L'énergie mécanique totale est également définie à une constante près : une propriété héritée de l'énergie potentielle.
L'existence d'une énergie potentielle est la signature d'un système conservatif (en
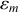) si
.
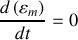Si cette égalité n'est pas vérifiée, le système n'est pas conservatif et deux situations sont possibles :
Une variation au cours du temps
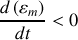mesurera une puissance dissipée par des forces de type "frottement".Cette variation est caractéristique de pertes d'énergie dans le système (dissipation) et d'irréversibilité comme en thermodynamique.
Si la variation est positive, ce résultat décrit un système ouvert et recevant de l'énergie de l'extérieur, comme celle d'un moteur.
