Attention :
Une propriété intrinsèque du fluide est sa viscosité.
Elle se manifeste à travers les forces de frottement s'exerçant entre les particules fluides en mouvement relatif. Associées aux forces de pression (normales aux surfaces), ces forces de frottement forment des contraintes comportant une composante normale et une composante tangentielle (parallèle à la surface). Ramenée à une surface élémentaire ![]() de normale
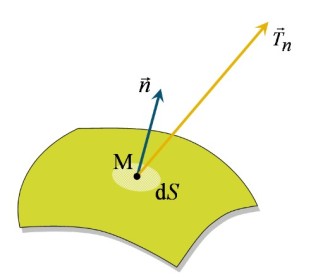
de normale ![]() , la force par unité de surface qui s'exerce en un point M est la contrainte notée
, la force par unité de surface qui s'exerce en un point M est la contrainte notée ![]() . On a donc :
. On a donc :
La contrainte ![]() (voir figure 8) présente une orientation a priori différente de celle de la normale
(voir figure 8) présente une orientation a priori différente de celle de la normale ![]() et que les dimensions de cette contrainte sont celles d'une pression (on l'exprimera donc en pascal ou en
et que les dimensions de cette contrainte sont celles d'une pression (on l'exprimera donc en pascal ou en ![]() ).
).
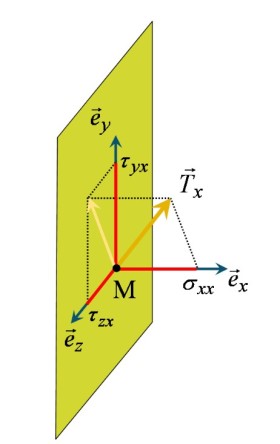
Pour fixer les idées, examinons le cas particulier d'une contrainte s'exerçant en un point d'une surface perpendiculaire à l'axe ![]() d'un repère cartésien. Cette contrainte,
d'un repère cartésien. Cette contrainte, ![]() , présente alors trois composantes : une composante normale, notée
, présente alors trois composantes : une composante normale, notée ![]() , et deux composantes tangentielles, notées
, et deux composantes tangentielles, notées ![]() et
et ![]() (voir figure 9). Par convention, le premier indice indique la direction portant la composante alors que le second indice se réfère à la normale à la surface subissant la contrainte. On peut donc développer
(voir figure 9). Par convention, le premier indice indique la direction portant la composante alors que le second indice se réfère à la normale à la surface subissant la contrainte. On peut donc développer ![]() comme :
comme :
De manière analogue, si l'on considère les contraintes s'exerçant sur des surfaces perpendiculaires aux axes ![]() et
et ![]() , on peut les exprimer respectivement :
, on peut les exprimer respectivement :
Par ailleurs, le théorème de Cauchy (non démontré ici) permet de formuler la contrainte s'exerçant sur une surface d'orientation quelconque ![]() , comme une combinaison linéaire de
, comme une combinaison linéaire de ![]() ,
, ![]() et
et ![]() :
:
En développant ![]() ,
, ![]() et
et ![]() , on obtient :
, on obtient :
et en regroupant les termes selon les trois directions de l'espace :
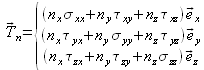
On note alors que ce résultat n'est autre que celui du produit d'un tenseur de rang 2 (matrice ![]() ) par la normale
) par la normale ![]() :
:

où ![]() est appelé tenseur des contraintes. Ce tenseur présente donc l'intérêt de pouvoir calculer directement la contrainte s'exerçant sur une surface d'orientation quelconque. On remarquera par ailleurs que les composantes normales se trouvent sur la diagonale du tenseur alors que les composantes tangentielles se trouvent de part et d'autre de la diagonale.
est appelé tenseur des contraintes. Ce tenseur présente donc l'intérêt de pouvoir calculer directement la contrainte s'exerçant sur une surface d'orientation quelconque. On remarquera par ailleurs que les composantes normales se trouvent sur la diagonale du tenseur alors que les composantes tangentielles se trouvent de part et d'autre de la diagonale.
Attention :
Ce tenseur est attaché à un point donné de l'espace fluide (il diffère a priori d'un point à un autre) et ses composantes sont attachées au repère dans lequel on a choisi de travailler. En fonction de la géométrie du problème à traiter, il pourra évidemment être plus approprié de travailler dans un repère cylindrique (voire même sphérique).
D'un point de vue mathématique, il est possible de décomposer un tenseur en la somme d'un tenseur sphérique et d'un tenseur de trace nulle. Dans le cas présent, cela conduit à écrire :![]() , ce qui, en développant, donne :
, ce qui, en développant, donne :
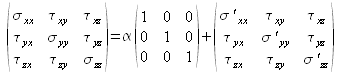
Cette décomposition impose donc :
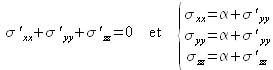
L'association de ces quatre relations conduit à fixer la valeur de la quantité scalaire ![]() :
:
Cette décomposition permet donc de reformuler ainsi la contrainte :
Il apparaît alors naturellement deux termes dans l'expression de la force :
où le premier des deux correspondant clairement à une force purement normale à la surface, laquelle peut facilement être identifiée à la force de pression hydrostatique. Ainsi, la quantité scalaire ![]() n'est autre que l'opposée de la pression hydrostatique :
n'est autre que l'opposée de la pression hydrostatique :
Puisque l'absence de viscosité (fluide parfait) conduirait naturellement à ne considérer que les forces de pression hydrostatique, le tenseur ![]() rend compte spécifiquement des forces dues à la viscosité : il prend donc l'appellation de tenseur des contraintes de viscosité.
rend compte spécifiquement des forces dues à la viscosité : il prend donc l'appellation de tenseur des contraintes de viscosité.




