Par définition, les fluides « newtoniens »
sont ceux pour lesquels les composantes du tenseur des contraintes de viscosité ![]() dépendent linéairement des composantes du tenseur des taux de déformation pure
dépendent linéairement des composantes du tenseur des taux de déformation pure ![]() . Autrement dit, pour simplifier, on peut dire que les déformations y sont proportionnelles aux contraintes. C'est notamment le cas pour la plupart des fluides usuels (on se limitera dans ce cours à l'étude des fluides newtoniens), sachant que les fluides non newtoniens sont presque tous des colloïdes (beaucoup plus complexes à étudier).
. Autrement dit, pour simplifier, on peut dire que les déformations y sont proportionnelles aux contraintes. C'est notamment le cas pour la plupart des fluides usuels (on se limitera dans ce cours à l'étude des fluides newtoniens), sachant que les fluides non newtoniens sont presque tous des colloïdes (beaucoup plus complexes à étudier).
Pour simplifier l'écriture des relations établissant la linéarité entre contraintes et déformations pures, on utilisera la notation contractée des éléments tensoriels. Ainsi, chaque élément d'un tenseur de rang 2 est identifié au moyen de deux indices,
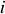 et
et
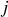 , se référant chacun à l'une des trois possibilités parmi
, se référant chacun à l'une des trois possibilités parmi
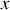 ,
,
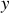 ou
ou
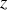 . On peut, à titre d'exemple, généraliser la formulation des éléments du tenseur des taux de déformation pure :
. On peut, à titre d'exemple, généraliser la formulation des éléments du tenseur des taux de déformation pure :
où la symétrie du tenseur apparaît clairement ![]() .
.
Pour un fluide isotrope, on pourra admettre la relation simple suivante entre les éléments ![]() du tenseur
du tenseur ![]() et ceux,
et ceux, ![]() , du tenseur
, du tenseur ![]() :
:
où ![]() est le symbole de Krönecker (
est le symbole de Krönecker (![]() et
et ![]() ),
),![]() est la viscosité et
est la viscosité et ![]() la viscosité de dilatation. On remarque par ailleurs que la somme des éléments diagonaux du tenseur des taux de déformation pure n'est autre que la divergence du vecteur vitesse :
la viscosité de dilatation. On remarque par ailleurs que la somme des éléments diagonaux du tenseur des taux de déformation pure n'est autre que la divergence du vecteur vitesse :
Or, lorsque le fluide étudié est incompressible et que son écoulement est conservatif, l'équation de continuité (voir chapitre précédent) conduit à annuler cette divergence : ![]() .
.
Il vient alors que :
montrant que les éléments de ![]() et ceux de
et ceux de ![]() sont directement proportionnels et que le coefficient de proportionnalité n'est autre que la viscosité du fluide. Ainsi, il est possible de revenir à une notation tensorielle formulant simplement :
sont directement proportionnels et que le coefficient de proportionnalité n'est autre que la viscosité du fluide. Ainsi, il est possible de revenir à une notation tensorielle formulant simplement :
Reprenons désormais l'équation fondamentale de la dynamique pour la reconsidérer dans l'hypothèse d'un fluide newtonien :
ce qui permet de formuler une relation où les contraintes n'apparaissent plus explicitement :
Il est ensuite possible de développer, pour la simplifier, l'expression de ![]() en faisant appel à la notation contractée :
en faisant appel à la notation contractée :
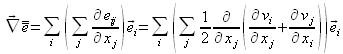
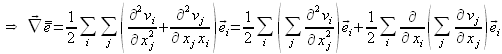
Cette réécriture a pour intérêt de faire apparaître l'opérateur laplacien sur chacune des composantes de la vitesse, ainsi que la divergence du vecteur vitesse :
Donc, on obtient :
Et puisque le fluide est considéré incompressible, on a ![]() , conduisant à :
, conduisant à :![]() .
.
Fondamental :
Dans l'hypothèse d'un fluide newtonien incompressible en écoulement conservatif, l'équation fondamentale de la dynamique prend donc la forme simplifiée suivante :
et constitue ce qu'on appelle communément l'équation de Navier-Stokes.
L'exploitation de cette formule (constituant l'équation fondamentale à partir de laquelle la plupart des écoulements pourront être décrits) implique le développement de l'expression du terme d'accélération. En effet, l'écoulement pouvant être non stationnaire, le vecteur vitesse peut, en un point fixe varier dans le temps (accélération instantanée). Par ailleurs, il faut que l'accélération puisse rendre compte de l'évolution du vecteur vitesse lorsqu'une particule fluide se déplace d'un point à un autre (accélération convective). Ces deux types d'accélération vont ainsi pouvoir être pris en compte à travers la notion de dérivée particulaire du vecteur vitesse :
Complément :
Considérons une quantité scalaire fonction à la fois du temps et des coordonnées d'espace : ![]() . Sa différentielle s'écrit :
. Sa différentielle s'écrit : ![]() . En divisant cette différentielle par
. En divisant cette différentielle par ![]() , on obtient la dérivée particulaire de
, on obtient la dérivée particulaire de ![]() :
:
où peut être introduit l'opérateur gradient ![]() sous la forme :
sous la forme :
Par projection sur les trois axes d'un repère, on peut obtenir une relation vectorielle analogue concernant le vecteur vitesse et ainsi obtenir l'expression de l'accélération particulaire.
Ainsi, l'équation de Navier-Stokes peut s'écrire explicitement de la manière suivante :
où, selon un repère cartésien tel que ![]() , les trois projections de cette équation se formulent :
, les trois projections de cette équation se formulent :
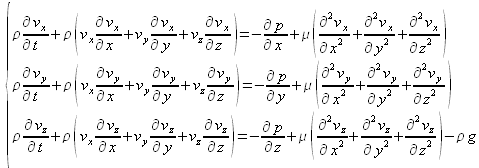
Dans un système de coordonnées cylindriques, avec toujours ![]() , on obtient de manière équivalente :
, on obtient de manière équivalente :
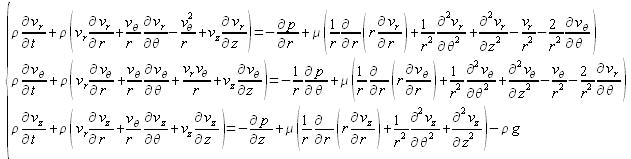
La connaissance de conditions aux limites, portant sur la vitesse et la pression, doit permettre de résoudre ce système d'équations et d'obtenir le champ de vecteurs vitesse. Néanmoins, on comprend facilement qu'une résolution analytique peut s'avérer difficile, voire même impossible. C'est pourquoi le recours à des résolutions numériques est souvent nécessaire pour appréhender des problématiques concrètes.
Une approche purement analytique peut toutefois permettre la description d'écoulements spécifiques, pour lesquels un certain nombre d'hypothèses simplificatrices peuvent être introduites. C'est le cas notamment lorsqu'un écoulement est stationnaire, laminaire ou bien lorsque le fluide peut être considéré parfait (viscosité négligeable).




