Compte tenu de ce qui vient d'être établi, il est maintenant possible d'évaluer l'ensemble des forces de surface s'exerçant sur un élément de volume fluide. Nous allons donc pouvoir appliquer le Principe Fondamental de la Dynamique (PFD) sur cet élément de volume, avec pour objectif de formuler une équation locale régissant le mouvement des particules.

Figure 10

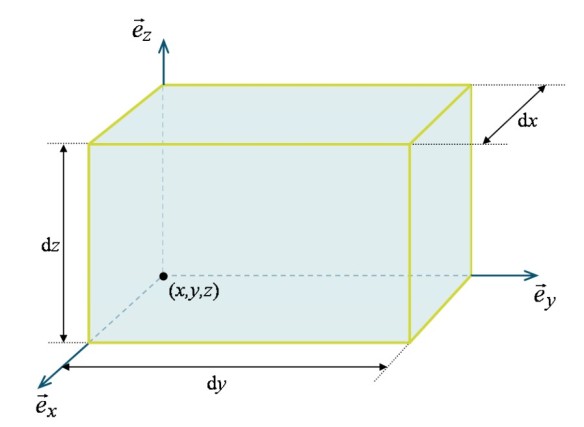
Pour simplifier le raisonnement, choisissons un élément de volume parallélépipède rectangle de dimensions , dont l'accélération vaut , dans un champ de pesanteur (voir figure 10). L'ensemble des forces s'exerçant sur le parallélépipède se subdivise en deux catégories : les forces de volume et les forces de surface. L'application du PFD conduit donc à :

Compte tenu du contexte, seul le poids constitue une force de volume : .

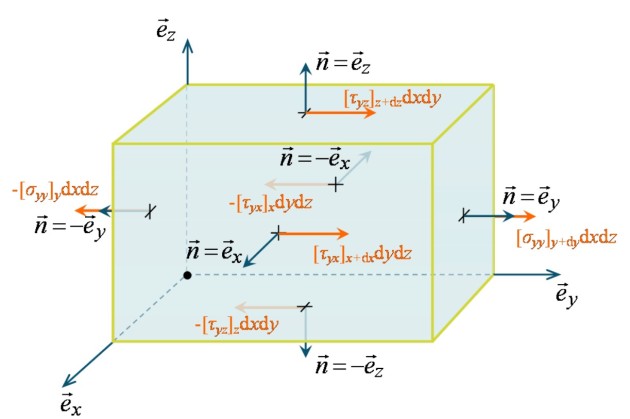
Il reste donc à formuler l'ensemble des forces de surface, lesquelles s'exercent sur les 6 faces du parallélépipède et donnent nécessairement 3 composantes : . Afin de simplifier l'approche, on peut dans un premier temps se contenter d'analyser la composante (on trouvera ensuite facilement les deux autres par analogie). Ainsi, chacune des 6 faces est soumise à une contrainte dont une des trois composantes contribue à dans la direction . Par exemple, la face supérieure (située en ) de normale est soumise à une contrainte dont la contribution selon se résume à . En terme de force, la contribution correspond à puisque l'aire de la face supérieure vaut . Le schéma de la figure 11 explicite l'ensemble des 5 autres contributions obtenues de manière analogue.

Figure 11

On obtient donc :

Les dimensions du parallélépipède étant petites, il est légitime de faire un développement limité au premier ordre du type :

ce qui conduit à la simplification de en :

Par analogie, on peut ensuite formuler les deux autres contributions :

D'un point de vue mathématique, on constate que est proportionnelle au volume et que chacune de ses composantes correspond à une somme des dérivées partielles des composantes du tenseur des contraintes. Une simplification d'écriture conduit à formuler :

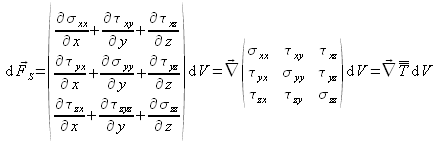
Il reste alors à reprendre l'équation rendant compte du PFD :

où, par simplification, le volume n'intervient plus. On obtient donc une équation locale :

À ce stade, il convient de développer le tenseur des contraintes pour faire apparaître explicitement la pression hydrostatique ainsi que les contraintes de viscosité. On utilise donc :

pour obtenir l'équation fondamentale de la dynamique des fluides :

Cette équation fondamentale de la dynamique des fluides va donc pouvoir servir de base générale pour établir des formulations plus spécifiques liées à la nature même du fluide (parfait, visqueux, newtonien...) ou au différents types d'écoulement (laminaire, turbulent, stationnaire...).