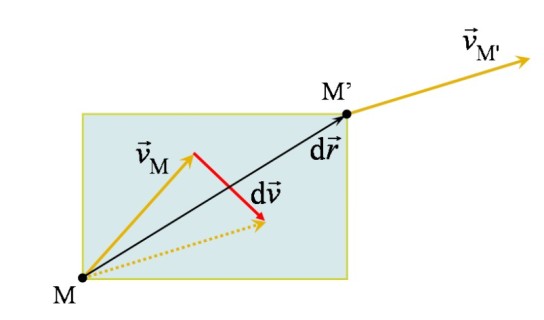
Au sein de l'écoulement, chaque particule fluide subit des changements de position, d'orientation et de forme. L'analyse de ces changements peut s'appuyer sur la comparaison des vitesses de deux points voisins appartenant à la même particule : considérons un point 
dont la vitesse est 
et un point 
dont la vitesse est 
. Si on pose 
, alors il est possible de définir l'accroissement de vitesse 
en explicitant :
formulation pouvant être illustrée à deux dimensions comme le montre la figure 12.
Par simple projection sur les axes d'un repère cartésien, un développement limité au premier ordre permet d'expliciter chacune des trois composantes de la vitesse en 
avec notamment l'accroissement de vitesse par rapport à celle en 
:
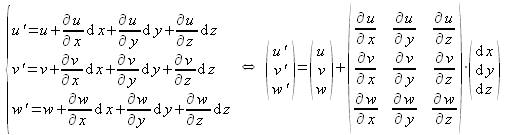
On introduit ainsi un nouveau tenseur, le tenseur des taux de déformation 
, tel que :
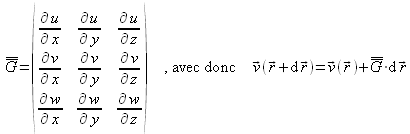
Toutes les informations concernant les déformations sont alors contenues dans les éléments de ce tenseur. Il convient donc d'identifier chacun de ces éléments.
Termes d'élongation
Supposons que seuls les éléments diagonaux soient non nuls et raisonnons, pour simplifier, à deux dimensions (écoulement plan perpendiculaire à l'axe z). Une particule bidimensionnelle, rectangulaire, de surface 
, est définie à l'instant
par les coordonnées de 4 points : 
; 
; 
; 
. Connaissant la vitesse du point A :
: , on peut en déduire les vitesses des 3 autres sommets pour finalement connaître la position de chacun des 4 points à l'instant 
:
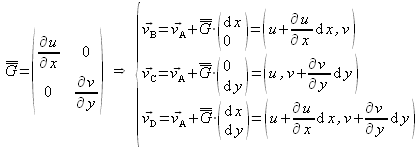
Ainsi, à l'instant 
:
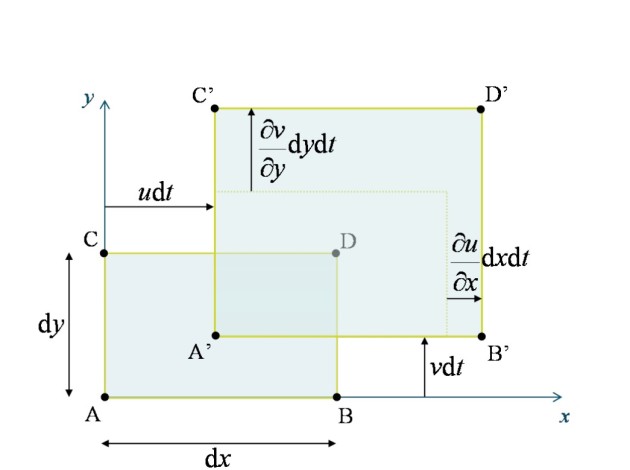
Compte tenu de ce résultat, l'illustration de la figure 13 permet de constater que la particule a globalement subi une translation, qu'elle reste de forme rectangulaire mais présente une élongation 
suivant l'axe x, et 
suivant l'axe
. Pendant le temps 
, la particule a donc subi un accroissement relatif de longueur de 
et 
, où 
et 
peuvent être définis comme des taux d'élongation.
Remarque :
Ces taux d'élongation peuvent être positifs ou négatifs (contraction). Par ailleurs, la variation relative de surface s'exprime :
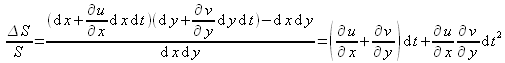
Les distances et temps étant petits, on peut négliger le terme de second ordre et reformuler la variation relative de surface comme :
. La généralisation de ce résultat à trois dimensions, permet donc d'exprimer la variation relative de volume (ou taux d'expansion du volume) de la particule fluide comme :
En conclusion, les éléments diagonaux du tenseur des taux de déformation correspondent aux taux d'élongation dans les trois directions de l'espace et permettent, à partir du calcul de la trace du tenseur, d'évaluer le taux d'expansion local du volume.
Termes de déformation angulaire et rotation
Supposons maintenant que seuls les éléments en dehors de la diagonale soient non nuls dans le tenseur des taux de déformation, et raisonnons encore une fois à deux dimensions à partir d'une particule rectangulaire ABCD :
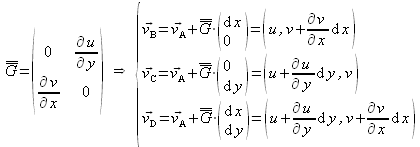
Ainsi, à l'instant 
:
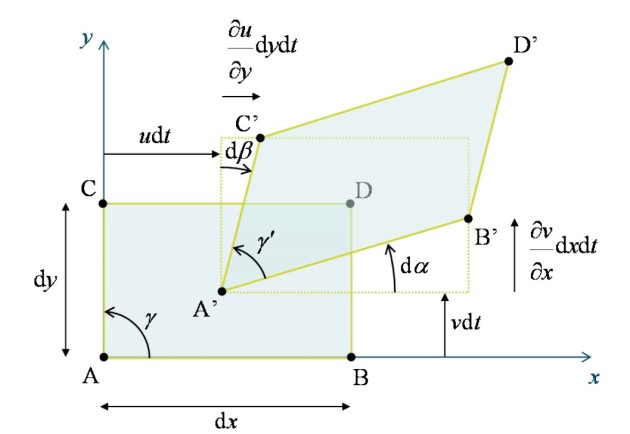
ce qui conduit à l'illustration de la figure 14, sur laquelle apparaît clairement une modification des angles en plus de la translation globale déjà observée. Cette déformation peut se formaliser au moyen de deux angles 
et 
tels que :
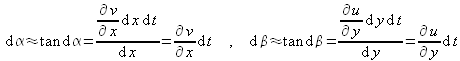
soit encore :
et 
. Il est maintenant possible d'envisager deux cas particuliers :
Les deux angles sont égaux :
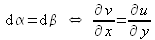.L'égalité rend le tenseur
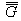symétrique, en même temps qu'elle concrétise une déformation angulaire pure au cours de laquelle l'angle 
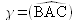subit une variation :
les deux angles s'opposent :
Le tenseur 
est de fait antisymétrique et conduit à la configuration illustrée figure 15. Il apparaît clairement que la particule n'est pas déformée 
mais subit une rotation pure d'angle 
autour de l'axe
.
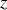Remarque :
Cet angle de rotation correspond, au facteur
près, à la composante suivant
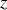du vecteur rotationnel de la vitesse :
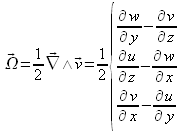
Appelé vecteur tourbillon, 
rend compte des rotations possibles de la particule fluide autour des trois axes que forme le repère cartésien.
Pour résumer, le seul tenseur 
est capable définir l'ensemble des déplacements et déformations qu'une particule fluide subit simultanément au sein d'un écoulement (voir figure 16). Or, d'un point de vue mathématique, ce tenseur est susceptible de se décomposer en la somme d'un tenseur symétrique 
et d'un tenseur antisymétrique 
:
Attention :
Le tenseur symétrique 
rend compte des élongations-contractions (éléments diagonaux) ainsi que des déformations angulaires pures (éléments hors diagonale) : ce tenseur reçoit l'appellation de tenseur des taux de déformation pure. On doit y ajouter le tenseur antisymétrique 
qui rend compte des rotations et s'appelle le tenseur des taux de rotations pures.
Concernant ce dernier tenseur, on identifiera facilement ses éléments aux composantes du vecteur tourbillon 
; on peut ainsi écrire :
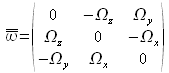
et montrer que :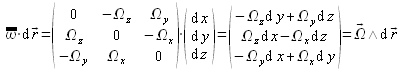 
.
Remarque :
Un écoulement sera qualifié d'irrotationnel lorsque 
. Dans ce cas les particules fluides ne subissent aucune rotation pure au sein de l'écoulement.
On a donc ainsi complètement défini le mouvement et la déformation d'une particule fluide, en termes de simple translation, élongation-contraction, déformation angulaire et rotation, en développant l'expression de l'accroissement de vitesse 
:
