L'équation de continuité est d'intérêt très général puisqu'elle traduit le principe de conservation de la masse au sein d'un écoulement. L'établissement de cette équation locale repose sur un bilan de masse de fluide au sein d'un élément de volume pendant un temps élémentaire . On considère alors un élément de volume parallélépipédique dont la masse est proportionnelle à la masse volumique du fluide et vaut donc : . De manière générique, la variation de masse pendant le temps peut se formuler :

Par ailleurs, cette variation de masse peut être identifiée à la somme algébrique des débits traversant les 6 faces du parallélépipède, augmentée (ou diminuée) des éventuels sources ou puits pouvant se trouver à l'intérieur du parallélépipède (ces sources ou puits sont des points de l'espace où de la matière fluide peut être créée ou détruite).

Figure 17

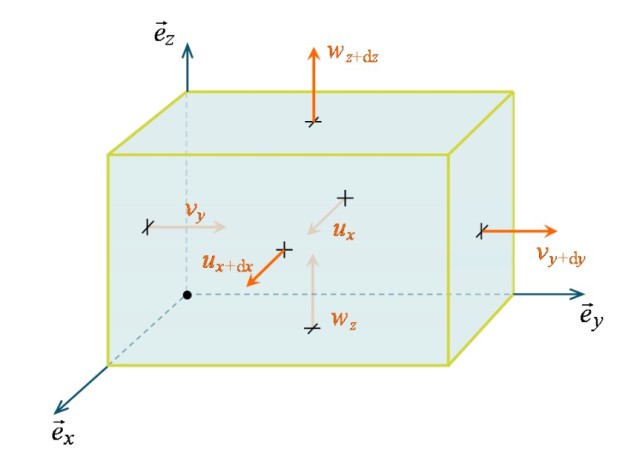
• Considérons dans un premier temps l'ensemble des débits traversant les 6 faces du parallélépipède, et raisonnons à partir du schéma de la figure 17. Le vecteur vitesse présente 3 composantes étant chacune perpendiculaire à 2 des 6 faces. Le débit massique à travers une surface correspond dans ce cas au produit de la masse volumique par la composante de la vitesse et par la surface traversée.

Par analogie, selon les deux autres directions on trouve :

Par conséquent, la variation de masse due aux débits massiques à travers les 6 faces se formule :

• S'il existe, au sein de l'élément de volume, des puits et des sources, ils sont caractérisés chacun par un débit volumique par unité de volume (bien que ponctuels, ils génèrent un débit volumique à l'intérieur de 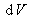). On les notera 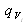et on pourra leur affecter des valeurs positives (sources) ou négatives (puits). Ainsi, le bilan de masse pendant le temps 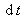créée ou détruite à l'intérieur du volume 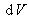s'exprime :

Il résulte de la prise en compte de ces différents termes la formulation suivante de la variation de masse du volume pendant le temps :

qui, après simplification par et , est ramenée à une équation locale connue sous l'appellation d'équation de continuité :

Il convient alors d'envisager quelques cas particuliers :

• si l'écoulement est stationnaire (aucune variation dans le temps des différentes grandeurs caractérisant l'écoulement et le fluide), alors on a :

• si l'écoulement est dépourvu de puits et sources, on dit qu'il est conservatif , et dans ce cas :

• si le fluide est incompressible , alors sa masse volumique est une constante (ne dépendant ni du temps, ni des coordonnées de l'espace) ; dans ce cas :

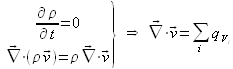
• si l'écoulement est conservatif et que le fluide est incompressible (il s'agit de la double hypothèse que l'on retiendra pour la plupart des écoulements étudiés dans ce cours), alors on a tout simplement :