Partons de l'équation de Navier-Stokes établie pour l'écoulement d'un fluide newtonien incompressible :
Si l'écoulement est stationnaire, la dérivée particulaire se résume à la dérivée convective et peut se développer comme :
On peut alors écrire :
L'accélération de la pesanteur dérivant d'un potentiel et le fluide étant incompressible, on regroupe sous un même gradient trois des cinq termes de cette équation pour lui donner la forme suivante :
On retrouve ainsi une formulation semblable à celle conduisant pour un fluide parfait à l'équation de Bernoulli. De la même manière, le produit vectoriel du vecteur vitesse avec le rotationnel de la vitesse s'annule lorsque l'équation est considérée sur l'ensemble des points constituant une ligne de courant. Il reste donc que le long d'une ligne de courant, l'écoulement stationnaire d'un fluide de viscosité non négligeable obéit à l'équation suivante :
La pression totale (également appelée « charge »
), notée 
, correspond à la somme des trois termes de pression se trouvant sous le gradient : 
. C'est donc une quantité scalaire qui doit vérifier l'équation :
Un écoulement laminaire étant caractérisé par un champ de vecteurs vitesse tous orientés dans la même direction, supposons qu'un repère cartésien soit choisi de telle sorte qu'en tout point de l'écoulement on ait 
. Dans ces conditions, la projection dans les trois directions du repère de l'équation précédemment établie, donne :
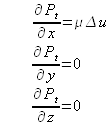
On en déduit que la pression totale n'est fonction que de 
, et qu'elle varie en obéissant à l'équation :
Par ailleurs, l'écoulement étant conservatif, l'équation de continuité s'applique dans sa forme la plus simple :
et comme 
, il en découle 
. Nous pouvons alors reconsidérer l'équation régissant l'évolution de la pression totale en la formulant :
Il s'avère alors que le membre de gauche ne peut dépendre que de 
alors que celui de droite ne peut dépendre que de 
et 
. La conséquence est donc que les deux membres sont égaux à une même constante. Ceci permet de montrer que la pression totale varie linéairement avec 
:
Remarque :
On notera que si la viscosité est négligée, la pression totale ne varie pas. En effet, la constante étant proportionnelle à 
, elle devient nulle, et on retrouve le contexte d'un écoulement de fluide parfait où l'équation de Bernoulli s'applique le long d'une ligne de courant :
on dit alors que la charge est constante ou bien encore qu'il n'y a pas de perte de charge.
En revanche, pour un fluide réel (dont la viscosité n'est pas négligeable), l'écoulement laminaire est caractérisé par une variation linéaire de la charge (ou pression totale) avec la distance parcourue. À ce stade, la logique peut déjà laisser supposer que la charge décroît et que par conséquent la constante est négative. En effet, puisque les frottements visqueux sont responsables d'une dissipation d'énergie et que la pression totale n'est autre qu'une énergie volumique, il s'ensuit logiquement que la pression totale doit diminuer avec la progression de l'écoulement (la démonstration en sera faite plus loin dans la cadre de l'écoulement de Poiseuille).
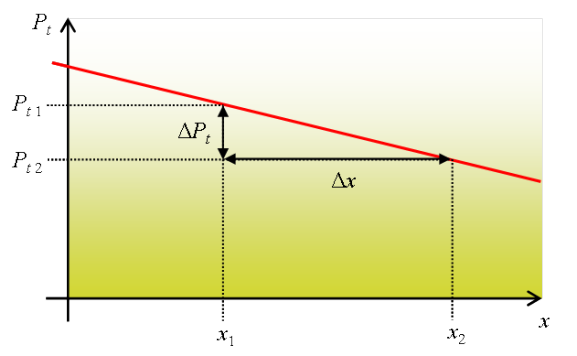
Dans l'hypothèse logique d'une pression totale diminuant linéairement avec la progression de l'écoulement, le graphe de la figure 28 montre que sur une longueur
la chute de pression totale 
est proportionnelle à 
et s'exprime :
Ainsi, une chute de pression totale (perte de charge) se traduit par 
et est la conséquence d'un gradient de pression constant et négatif. C'est pourquoi on parle de pertes de charges régulières.
En pratique, la quantification de ces pertes de charge requiert la détermination du gradient de pression totale en fonction des paramètres caractérisant le fluide et l'écoulement. Après quoi, il est commode de généraliser l'équation de Bernoulli en y faisant apparaître les pertes de charges régulières de la manière suivante :
