Il est d'usage d'exprimer une perte de charge en fonction de la pression cinétique de l'écoulement dans la conduite. La pression cinétique est générée par le mouvement (elle correspond à l'énergie cinétique par unité de volume) et s'exprime : . La vitesse peut être considérée comme la vitesse moyenne dans la conduite dans la mesure où la pression cinétique exprimée est aussi une valeur moyenne. Dans ces conditions, on peut formuler la perte de charge sur une longueur d'une conduite de rayon comme :

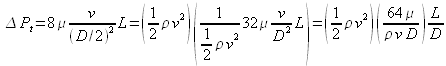
où apparaît le nombre de Reynolds caractérisant l'écoulement :

Ainsi, la perte de charge s'exprime :

où le rapport est un nombre sans dimension qui prend le nom de coefficient de perte de charge régulière. À partir de résultat, on peut généraliser cette formulation en exprimant toute perte de charge sur une longueur de conduite de diamètre comme :

On met ainsi en évidence que les pertes de charge régulières sont proportionnelles à la pression cinétique, à une grandeur sans dimension caractérisant la conduite , et au coefficient de perte de charge régulière caractérisant l'écoulement et qui, lorsqu'il est laminaire ( ), se formule comme .

Figure 31

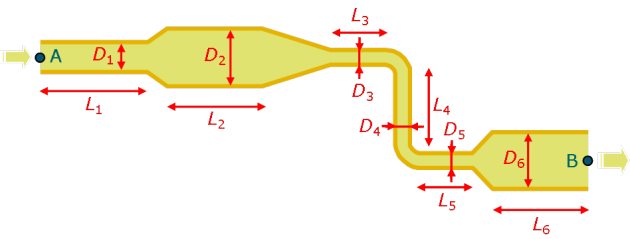
D'un point de vue pratique, cette formulation est particulièrement adaptée pour évaluer l'ensemble des pertes de charge occasionné par un circuit hydraulique comportant une succession de différents tronçons de conduite, comme l'illustre le schéma de la figure 31. La différence de pression totale entre l'entrée et la sortie du circuit est la somme de deux types de contribution :

• les pertes de charge dues aux singularités que sont les changements de direction et les changements de diamètre (rétrécissements et élargissements) ;

• les pertes de charge régulières dues aux frottements visqueux.

Les premières seront étudiées plus loin. Les secondes se formulent comme la somme des pertes occasionnées par chaque tronçon :