L'objectif est ici de caractériser les pertes de charge régulières en considérant un écoulement spécifique. Considérons alors l'écoulement laminaire d'un fluide de viscosité et de masse volumique , dans une conduite cylindrique de rayon , posée horizontalement. Le schéma de la figure 29 explicite cette configuration et permet de définir un repère cylindrique dont l'axe de révolution est celui de la conduite et correspond à la direction de l'écoulement laminaire.

Figure 29

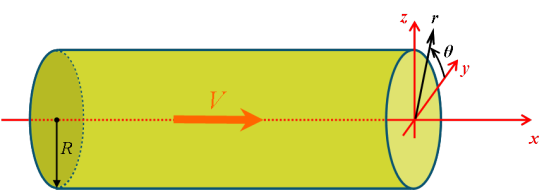
Dans ces conditions, l'écoulement étant laminaire, le vecteur vitesse en tout point s'écrit :

Par ailleurs, l'écoulement étant conservatif et le fluide incompressible, l'équation de continuité se résume à et se développe en coordonnées cylindriques comme :

Et puisque , il reste :

traduisant le fait que la vitesse n'évolue pas le long de l'axe de la conduite.

Compte tenu de la symétrie de révolution du problème, on en déduit par ailleurs que , ce qui permet d'en conclure que le vecteur vitesse est purement axial et ne dépend que de :

Reprenons maintenant l'équation régissant l'évolution de la pression totale le long d'un écoulement laminaire orienté suivant l'axe (voir section précédente) :

et développons l'expression du laplacien en tenant compte du fait que ne dépend que de :

On obtient donc :

où le terme de gauche ne dépend que de et celui de droite que de . Il s'en suit que les membres de cette équation sont égaux à une même constante K (voir discussion dans la section précédente). Ainsi, on a :

traduisant la perte de charge régulière ;

permettant la détermination du profil de vitesse .

Résolvons cette dernière équation pour établir le profil de vitesse sur une section de la conduite :

et donc :

et sont deux constantes d'intégration dont l'indétermination peut être levée en utilisant les conditions aux limites. Ainsi, on sait que la vitesse des particules fluides est nécessairement nulle au contact avec les parois de la conduite. On a donc :

Par ailleurs, sur l'axe de la conduite, en , la vitesse est nécessairement finie, ce qui impose d'avoir , sans quoi . Il en résulte que :

et que le profil de vitesse se formule :

On montre ainsi qu'il s'agit d'un profil parabolique et que impose . Le schéma de la figure 30 matérialise ce profil de vitesse caractérisé par une vitesse nulle aux parois et maximale sur l'axe ().

Figure 30

On comprend alors qu'à travers la constante , les pertes de charges régulières sont liées à la vitesse maximale, ou plus globalement à la vitesse moyenne de l'écoulement.

Si on définit la vitesse moyenne de l'écoulement comme le rapport du débit volumique sur la section de la conduite, on a :

avec , d'où :

et donc :

Et comme , on a par ailleurs :

Cette dernière relation permet ainsi de faire le lien entre le débit volumique et les pertes de charge régulières puisque et que , où . On obtient alors la formule de Poiseuille :

La différence de pression totale (ou perte de charge) engendrée par les frottements visqueux dans une conduite de longueur est donc proportionnelle à , mais également au débit et à la viscosité du fluide : .