Le long d'un réseau hydraulique, les singularités se caractérisent par des changements de géométrie se produisant localement. Il s'agit par exemple de modifications du diamètre de la conduite (rétrécissement ou élargissement), de changements de direction (coudes), de vannes, clapets etc. Bien évidemment, ces singularités sont à l'origine de dissipations d'énergie qui se traduisent par des pertes de charge, dites « singulières »
, venant s'ajouter aux pertes de charge régulières précédemment décrites.
Nous allons ici traiter le cas simple d'un élargissement brusque et, sous couvert d'un certain nombre d'hypothèses simplificatrices, formuler de manière analytique les pertes de charge engendrées par cette singularité typique.
Le raisonnement que nous utiliserons fait appel à un théorème d'intérêt très général pour traiter un grand nombre de problèmes en mécanique des fluides : il s'agit du théorème d'Euler. Nous proposons donc, en préambule et sous la forme d'un complément, d'exposer ce théorème.
Complément : « théorème de transport de Reynolds » et « théorème d'Euler »
Ces deux théorèmes s'appliquent dans le cadre de raisonnements portant sur le volume d'un système fluide en mouvement. De manière générale, considérons pour commencer une quantité scalaire fonction des coordonnées de l'espace et du temps : 
. Notons 
la quantité scalaire correspondant à l'intégrale de 
sur le volume 
d'un système constitué d'un ensemble de particules fluides, de sorte que :
Pour évaluer les variations de 
dans le temps, il nous faut calculer sa dérivée :
où la dérivée de l'intégrale porte aussi bien sur la fonction 
que sur le volume 
puisque ce dernier est susceptible d'évoluer dans le temps dans la mesure où le fluide est en mouvement (
). La méthode proposée consiste à considérer un volume de contrôle fixe,
, délimité par une surface de contrôle fermée et fixe, 
, à travers laquelle sera évaluer le flux de 
. Notons que typiquement on choisira 
à partir du volume 
à un instant 
donné. Dans ces conditions, on peut formuler le théorème de transport de Reynolds :
où le premier terme décrit les variations instantanées de 
(dérivée instantanée), alors que le deuxième terme décrit le flux de à travers la surface de contrôle (dérivée convective).
À titre d'exemple, on peut choisir la masse volumique 
comme fonction scalaire, de telle sorte que 
correspond à la masse d'un système fluide de volume 
. Le théorème de transport permet alors d'exprimer la variation de masse du système comme :
où l'intégrale en surface peut être transformée en intégrale volumique par application de la transformation d'Ostrogradski :
On reconnaît alors une partie de l'équation de continuité (voir partie A.4) qui, dans le cas d'un écoulement conservatif (sans puits ni source) conduit à : 
et confirme naturellement que 
, autrement dit que la masse est conservée.
Le raisonnement qui vient d'être exposé et qui concerne une quantité scalaire peut directement être transposé à une quantité vectorielle. Plus particulièrement, appliqué à la quantité de mouvement 
d'un système de volume 
, le théorème de transport de Reynolds conduit au théorème d'Euler :
où la dérivée par rapport au temps de la quantité de mouvement du système correspond à l'ensemble des forces extérieures s'exerçant sur le système. Or, cet ensemble de forces peut être décomposé en deux catégories : les forces de surface 
et les forces de volume qui typiquement se résument au poids du système 
. Dans le cas particulier d'un écoulement stationnaire (
), il reste :
D'un point de vue pratique, cette formulation permet de façon indirecte (mais simple) d'évaluer les forces de surface compte tenu du fait que le poids, aussi bien que le débit de quantité de mouvement, sont de loin plus faciles à calculer que l'intégrale surfacique du tenseur des contraintes.
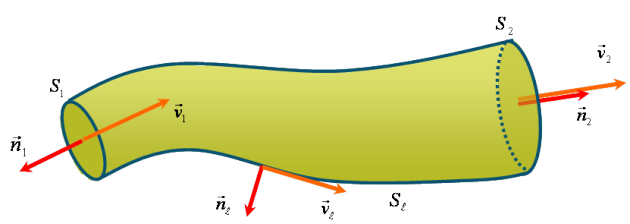
Toujours dans l'hypothèse d'un écoulement stationnaire, considérons comme volume de contrôle un tube de courant présentant une section amont 
où la vitesse sera supposée uniforme et notée 
, et une section aval 
où la vitesse 
est également uniforme (voir figure 34).
Par définition du tube de courant, il y a conservation du débit massique entre l'entrée et la sortie, de sorte que 
, et si le fluide est incompressible (
) on en déduit que 
. Compte tenu du volume de contrôle choisi, la surface de contrôle associée est composée des deux sections 
et 
ainsi que de la surface latérale 
. On peut donc formuler :
où 
en tout point de la surface latérale puisque celle-ci est constituée de lignes de courant le long desquelles la vitesse est tangentielle. Il en résulte :
avec
et 
, d'où :
La conservation du débit permet alors d'utiliser 
et d'aboutir à la formulation du théorème d'Euler :
Il s'agit donc d'un théorème très utile puisqu'il permet le calcul des résultantes des forces surfaciques (notamment de frottements) à partir de la connaissance du poids du système fluide et des vitesses en amont et en aval.
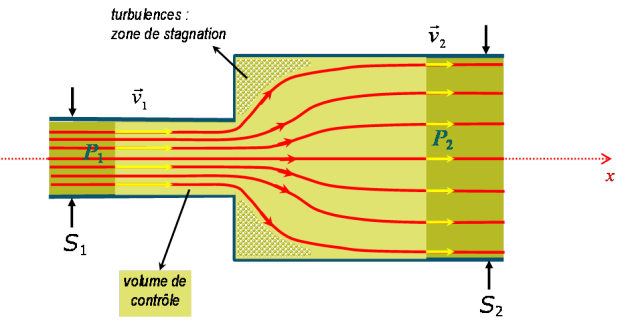
L'élargissement brusque schématisé sur la figure 35 est le siège de pertes de charge dues à la présence de zones de turbulences. Elles résultent du changement brusque de direction imposé au fluide, qui sous l'effet de sa propre inertie, ne peut suivre de près les contours de la paroi. Ces zones de turbulences sont donc dissipatrices d'énergie mais ne participe pas à l'écoulement global puisqu'en moyenne la vitesse y est nulle : ces zones sont aussi appelées « zones de stagnation »
.
La perte de charge engendrée par cette singularité peut alors s'évaluer de façon analytique en faisant appel au théorème d'Euler. Pour ce faire, considérons comme volume de contrôle l'espace occupé par le fluide entre la section amont 
et la section aval 
. Faisons par ailleurs l'hypothèse de vitesses et de pressions uniformes sur ces sections. On a donc :
que l'on peut projeter sur un axe horizontal (celui de la conduite) pour obtenir :
La résultante 
des forces de surface s'exerçant suivant 
est alors constituée des forces de pression s'exerçant sur des surfaces dont la normale est orientée suivant . Nous pouvons donc lister :
la poussée en amont
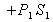, la contre-poussée en aval
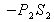,la force de pression s'exerçant sur la surface annulaire
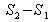qui, de fait, est la surface de la paroi en contact avec les zones de stagnation. Pour cette troisième force, on peut donc utiliser les lois de l'hydrostatique et en déduire que la pression qui s'exerce est approximativement la même que celle qui s'exerce en amont, soit 
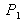. En effet, les différences d'altitude étant négligeables, la pression est pratiquement uniforme sur toute la section 
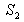au niveau de l'élargissement. Par conséquent, la troisième force de pression s'exprime :
.
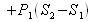On obtient donc :
ce qui se simplifie en :
En explicitant le débit massique en fonction de la vitesse de l'écoulement en aval, on a :
Ensuite, par un jeux d'écriture, on peut transformer cette égalité en faisant apparaître distinctement les pressions statiques et cinématiques en amont et en aval :
où les trois derniers termes du membre de droite peuvent se regrouper sous la forme d'une différence au carré :
Cette dernière formulation fait apparaître, d'une part la pression totale en amont 
, d'autre part la pression totale en avale 
, ainsi que la différence entre les deux 
constituant ainsi l'expression analytique de la perte de charge générée par la singularité. Cette perte de charge peut aussi se formuler en fonction de la pression cinétique de l'écoulement amont :
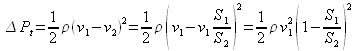
On peut ainsi introduire un coefficient sans dimension, fonction uniquement de la géométrie de la singularité, en l'occurrence ici des sections amont et aval :
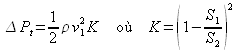
Ce résultat est généralisable à n'importe quel type de singularité dans la mesure où le coefficient de perte de charge singulière 
est connu. Dans ces conditions, pour un réseau hydraulique complet (voir figure 31) comportant différents tronçons de longueurs et sections différentes et reliés entre eux par des singularités, on peut évaluer les pertes de charge totales entre l'entrée et la sortie du circuit en formulant l'équation de Bernoulli généralisée :
Remarque :
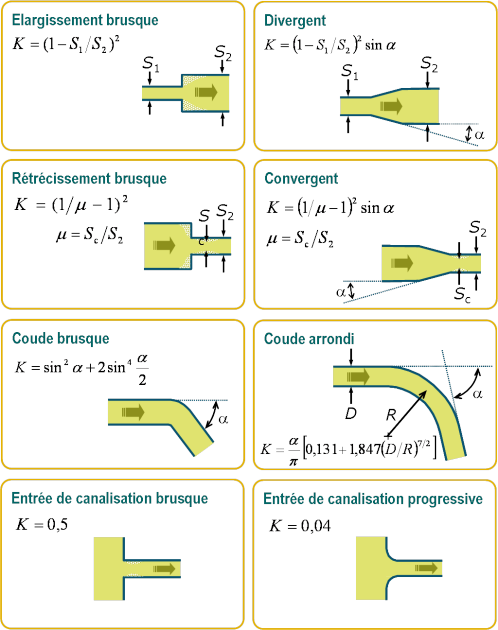
La plupart des singularités ne permettent pas une approche analytique simple comme celle qui vient d'être développée concernant l'élargissement brusque. Les coefficients de perte de charge sont donc le plus souvent déduit de mesures ou de calculs numériques, et sont disponibles sous forme d'abaques. À titre d'exemple, la figure 36 liste de façon non exhaustive quelques singularités typiques avec les coefficients de perte de charge associés.
