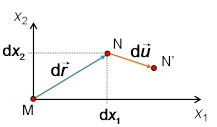
Isolons cette action en considérant que . Supposons ensuite que le repère soit choisi de telle sorte que et faisons l'hypothèse d'un point M ne subissant pas de déplacement : . En première approche, un raisonnement à deux dimensions suffira à analyser une déformation pure ; l'extrapolation à trois dimensions permettra ensuite de généraliser l'analyse. Choisissons donc un point N, voisin de M, les deux étant contenus dans le plan  ; on a ainsi : et le déplacement de N coïncide avec l'accroissement de déplacement : . Dérivée de la configuration générale de la figure 14, cette configuration particulière est explicitée figure 15.

Étudions spécifiquement les termes diagonaux du tenseur des déformations pures, en considérant que est purement diagonal :

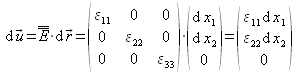
ce qui engendre la déformation explicitée figure 16.

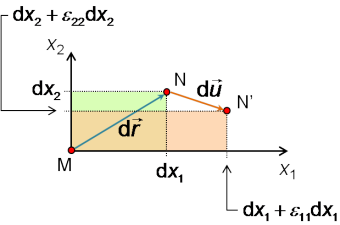
On obtient donc un allongement relatif suivant : ,

un allongement relatif suivant : ,

et par extrapolation selon la direction on aurait : .

Revenons à la configuration simplifiée d'une déformation à deux dimensions et évaluons la variation relative de surface. Avant déformation, la surface est définie comme  ; après déformation, elle s'explicite : . La variation relative de surface se formule alors :

soit, après simplification :

En généralisant à trois dimensions, on peut donc formuler la variation relative de volume comme :

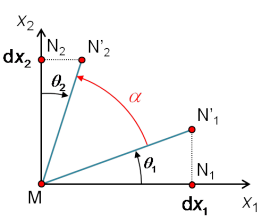
Étudions à présent l'action des termes non-diagonaux du tenseur et choisissons deux points et voisins de M et définissant deux directions orthogonales de telle sorte que et (figure 17). Sous l'action du tenseur des déformations pures, les déplacements de et peuvent respectivement se définir comme :

et s'expliciter comme :

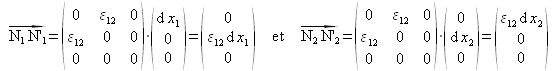
Comme le montre la figure 17, les déplacements qui en résultent génère une distorsion angulaire puisque les deux directions orthogonales définies par et viennent à former un angle tel que :

Les angles et étant par définition petits, on peut estimer que :

Il en résulte que : , résultat qui peut se généraliser à trois dimensions en identifiant chacun des éléments non-diagonaux du tenseur des déformations pures à une distorsion angulaire dans un des trois plans définis par le repère .