Le tenseur constitue la contribution antisymétrique du tenseur des déformations . Il ne comporte par conséquent que trois éléments indépendants non nuls :

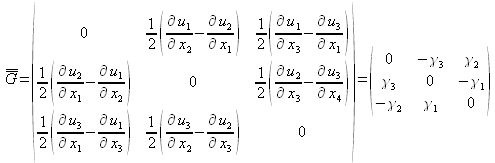
Ces trois éléments sont de fait les trois composantes d'un vecteur appelé « vecteur rotation », lequel correspond explicitement à la moitié du rotationnel du vecteur déplacement :

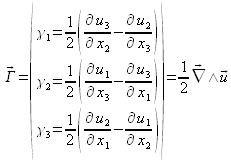
La contribution de à l'accroissement de déplacement s'exprime alors comme et s'explicite :

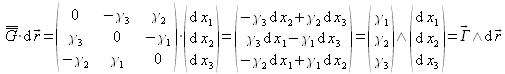
On a donc :

En reprenant le contexte de l'analyse des éléments non-diagonaux du tenseur des déformations pures, on peut graphiquement interpréter l'action des éléments du tenseur . Prenons le cas où seul est non nul et examinons ce qui résulte des déplacements des points et (figure 18) :

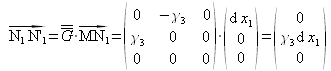
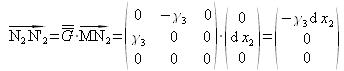
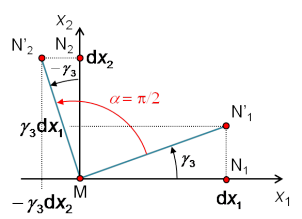
On constate ainsi qu'il n'y a pas de distorsion angulaire :

car les deux directions orthogonales définies par et restent orthogonales sous l'action de : . Par ailleurs, ces deux directions ont subi une rotation d'angle autour de l'axe donné par . Ce résultat est bien évidemment généralisable et permet d'interpréter l'effet de chacun des trois éléments du tenseur des rotations pures.