Les vitesses de propagation établies précédemment supposent que le milieu est infini, ou tout du moins de dimensions très grandes devant la longueur d'onde propagée. Dans le cas d'un milieu limité, comme par exemple une éprouvette, l'onde transversale se propage à la même vitesse (
) alors que l'onde longitudinale présente une célérité différente (
). Caractérisons cette célérité spécifique en raisonnant sur un échantillon de forme cylindrique, de section 
, et dont l'axe correspond à la direction de propagation longitudinale (on pourra arbitrairement choisir 
).
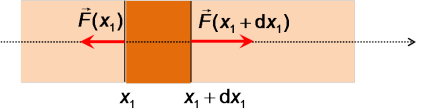
Comme l'illustre la figure 26, considérons une tranche de ce cylindre, située en 
, d'épaisseur 
, et subissant sur chacune de ses faces une force normale que l'on peut expliciter comme :
En appliquant le principe fondamental de la dynamique sur cette tranche, on peut formuler :
En simplifiant par 
et en développant au premier ordre 
, on obtient :
devenant donc une équation locale où la contrainte d'extension 
peut s'expliciter en fonction de l'allongement relatif et donc du déplacement 
. On utilise ainsi :
ce qui conduit à l'équation de propagation suivante :
Une telle équation de propagation est alors caractérisée par une célérité :
Remarque :
Les rapports de célérité au sein d'un même matériau ne dépendent que de son seul paramètre de Poisson 
. En effet, on peut expliciter les trois célérités possibles en fonction de 
, et 
:
On vérifie ainsi que :
confirmant d'une part que la célérité d'une onde longitudinale est toujours plus grande d'au moins un facteur 
que celle d'une onde transversale dans un même solide « illimité »
, et montrant d'autre part qu'une onde longitudinale se propage toujours plus lentement dans un solide de dimensions finies que dans un solide « illimité »
.
A titre d'illustration, prenons l'exemple de l'acier dont les propriétés mécaniques peuvent se résumer à : 
, 
et 
. L'application des formules établies précédemment permet de trouver les célérités suivantes :
avec 
et 
.
