Le formalisme lagrangien, développé jusqu'à présent, introduit une fonction de variables généralisées (coordonnées et vitesses associées) décrivant le système physique et minimisant l'intégrale d'action.
La fonction de Lagrange restant à élaborer et avec l'exemple de l'optique géométrique, cette fonctionnelle dépend du système à décrire.
Dans la hiérarchie des problèmes de mécanique, le plus simple à décrire est celui de la particule libre. Sous entendu, libre de toute interaction.
Son lagrangien devrait présenter la même simplicité originelle permettant, pour son élaboration, d'appliquer l'association 'particule libre - référentiel galiléen'.
Ce paragraphe s'inspire du syllabus de "L. Landau et E. Lifchitz" : Mécanique.
Son double coté, intuitif et mathématique, est paradoxal et séduisant.
En effet cette approche s'appuie sur les concepts intuitifs de référentiels galiléens, décrits comme des espaces homogènes et isotropes : ce sont les seuls à même de maintenir en l'état une particule libre.
Les conséquences pour le lagrangien de la particule libre sont immédiates : une particule ne pouvant être libre que dans un référentiel galiléen, toute translation rectiligne uniforme devrait laisser invariante la description lagrangienne.
Propriété : Des mathématiques, des mots et des conséquences physiques.
Dans une fonctionnelle, la dépendance des variables peut être explicite ou implicite.
Ainsi la fonction de Lagrange dépend en général des grandeurs positions, vitesses et temps selon :
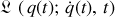
Dans ce formalisme, les positions et vitesses, décrivant le mouvement, sont considérées comme des variables indépendantes entre elles.
La variable "temps" est particulière par
sa réalité physique : incontournable, elle s'égrène, mais surtout
le mouvement a lieu pendant son écoulement : les variables du système en dépendent.
Ainsi pour toute fonctionnelle de ce type, l'évolution au cours du temps est décrit par une somme de variations.
Le total de ces variations ou dérivée totale au cours du temps se construit par les contributions additives suivantes :
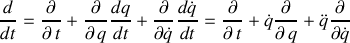
La première contribution exprime une dépendance explicite et les deux suivantes, des dépendances implicites, via les variables généralisées et modulées par leurs propres dépendances.
Ainsi dans la fonctionnelle, le temps est toujours présent, au moins implicitement.
Lors d'un mouvement, vitesses et positions varient en fonction du temps, qui s'écoule.
Par contre la dépendance explicite est moins avérée ; elle est relative au système étudié.
En mécanique classique, sa présence aide à différentier deux classes de problèmes.
L'absence de la "variable" temps caractérise une propriété essentielle : la conservation de l'énergie mécanique totale. Les systèmes sont soumis à des forces conservatives.
Ce sont des systèmes fermés, conservatifs.
Ceci sera explicité et développé dans le Chap. V B.
En termes de variations, la dépendance explicite, décrite par la dérivée partielle, est une contribution directe et parmi d'autres, plus ou moins importantes.
Ainsi une variable est "neutre" dans une fonction si elle n'apparaît pas explicitement.
En effet, les variations uniformes de cette variable soit ne produiront aucun effet soit auront un effet constant sur la variation de la fonction.
La variable devient alors "invisible" dans la fonction puisqu'elle ne produit pas d'effet (de variation) "remarquable et direct".
Et la notion d'invariance se met en place.
Ces outils mathématiques étant mis en place, deux autres images aident à mettre en place les concepts qui suivent.
1) Plus généralement en mécanique, la principale source de variation est l'interaction : elle permet le mouvement à partir d'un état statique.
L'absence d'interaction est un cas particulier de conservation de l'énergie mécanique totale, constituée alors uniquement par l'énergie cinétique. L'énergie potentielle n'apparaît plus dans la fonctionnelle "énergie mécanique".
L'absence d'interaction décrit également la particule libre, laquelle peut être en mouvement rectiligne uniforme.
2) Dans le cas d'un référentiel galiléen, le temps s'écoule de manière uniforme à l'infini, identique d'un référentiel galiléen à l'autre.
L'échelle de temps est invariante d'un référentiel à l'autre.
Elle ne peut constituer une source de variations en l'absence d'interaction.
Explication : Particule libre et référentiel galiléen.
En général, le lagrangien d'une particule en mouvement dans l'espace réel dépend, outre du temps, de la position et de la vitesse de la particule :

Mais une particule libre ne peut continuer à évoluer librement que dans un référentiel galiléen.
Exprimé autrement, toute particule libre est porteuse d'un référentiel galiléen.
Les caractéristiques d'un tel référentiel s'expriment en termes d'échelle
de temps : elle est uniforme, et
d'espace, homogène et isotrope.
Une particule libre, dans un tel référentiel, est alors soit au repos soit en mouvement rectiligne uniforme.
Indéfiniment.
Toute modification des caractéristiques ci-dessus trouve ses justifications dans des interactions (ce n'est plus une particule libre) ou des conditions extérieures au système (référentiel non galiléen).
Ainsi pour garantir un mouvement libre dans tout référentiel galiléen, des conditions, associées à des propriétés d'espace, se répercutent sur le lagrangien de la particule.
L'uniformité du temps caractérise son écoulement régulier et une échelle de temps constante.
Mathématiquement et pour décrire une particule libre, le lagrangien ne dépend pas explicitement du temps : les variations d'échelle pouvant influer sur le mouvement de la particule libre n'existent plus.
Dans un espace homogène, les distances parcourues par la particule libre pendant des durées régulières restent égales.
Ceci implique une invariance par translation et le lagrangien est indépendant de toute forme de distance, donc du module de
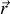 et de ses puissances.
et de ses puissances.Dans un espace isotrope, toutes les directions de l'espace sont équivalentes.
Le mouvement ne peut changer de direction après un choix initial et il est identique quelle que soit la direction choisie.
Il s'agit là d'une invariance par rotation, associée aux angles et donc à une forme vectorielle des variables.
En résumé, le lagrangien d'une particule libre ne dépend explicitement
d’aucune forme vectorielle, de position
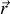 ou de vitesse
ou de vitesse
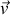 ,
, ni du module de la position,
ni du temps.
Fondamental :
L'hypothèse la plus simple pour la forme du lagrangien est donc :
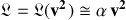
La dernière quasi-égalité est compréhensible si les puissances supérieures paires peuvent être négligées ou ignorées comme pour les faibles vitesses.
Mais ce ne sera pas nécessaire.
Cette forme de lagrangien doit être invariante lors du passage d'un référentiel galiléen à l'autre.
Ceci fera l'objet du paragraphe suivant.




