Soient deux référentiels
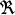et
en déplacement rectiligne uniforme, l’un par rapport à l’autre, à la vitesse
.
La particule libre se déplace à une vitesse
dans le référentiel
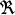et
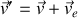dans
.
Dans un premier temps, l'inégalité entre les normes est supposée vérifiée selon :
.
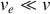Le lagrangien dans
s'écrit :
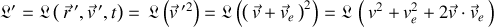
L’inégalité entre les modules des vitesses permet un développement limité au voisinage de
.
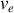La variable
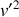est déjà notée comme suit :
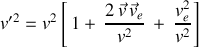
La variable de la fonctionnelle
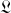étant
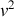, la fonctionnelle lagrangienne
est développée au premier ordre en
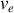pour obtenir :
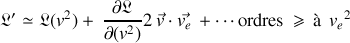
Les deux lagrangiens
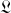et
peuvent être égaux (et la forme de fonctionnelle en
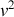validée) si le terme correctif au premier ordre peut être assimilé à la dérivée suivante :
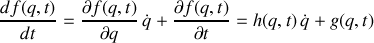
pour une situation à un degré de liberté et également dans le cas le plus général.
La présence multiplicative du vecteur vitesse
, représentant la composante en
dans le terme correctif, ainsi que la dépendance uniquement en
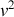du lagrangien permettent de conclure que :
la condition est réalisée si
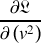ne dépend pas de la vitesse.
Cette dérivée est donc constante, et cela quelle que soit la forme de
.
Ce résultat valide la forme mathématique du lagrangien
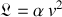pour la particule libre, dans tout référentiel galiléen.
Remarque :
Le symbole
a été remplacé par
puisque ce lagrangien est valide dans sa forme exacte : les puissances supérieures de
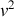ne peuvent exister.
De même, si la vitesse relative de translation des référentiels n'est pas faible, le développement limité en
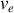peut être prolongé aux ordres supérieurs.
Cette opération fait apparaître des dérivées supérieures en
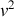de
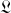... qui sont identiquement nulles.
Ainsi la condition
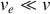, à l'origine du développement limité, peut être relaxée.
