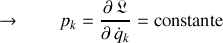La fonction de Lagrange pour un système fermé quelconque est notée:
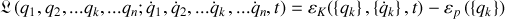
où les ensembles
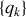et
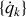représentent l'ensemble des variables (coordonnées ,vitesses) généralisées.
Définition : Coordonnée cyclique
La coordonnée
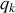est dite cyclique si le lagrangien ne dépend pas explicitement de
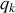soit
.
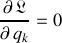L'équation du mouvement d'Euler-Lagrange associée à cette coordonnée généralisée permet de conclure pour l'impulsion généralisée correspondante
Elle est constante et conservée au cours du temps.
Exemple : Coordonnées cycliques et lois de conservation.
La variable cyclique, telle que définie ci dessus, est à comparer avec la variable neutre présentée dans le développement du lagrangien de la particule libre.
En mécanique, les deux cas identifiés pour les coordonnées produisent les résultats suivants :
Si la coordonnée
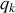est une distance, une longueur, par exemple
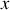, la quantité de mouvement, ou impulsion généralisée associée,
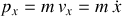est conservée. Cette propriété entraîne une invariance par translation le long de cette direction, et un mouvement uniforme en mécanique classique.
Si la coordonnée
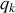est une variable angulaire, par exemple
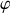des coordonnées cylindriques, l’impulsion associée
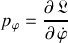est conservée.Elle correspond à la composante, relative à la rotation
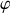, du moment cinétique,
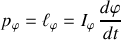. Ce moment cinétique, porté par l'axe
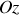, décrit un mouvement dans le plan
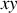et est constant.Cette loi de conservation entraîne une invariance par rotation.
Rappel :
Pour la variable angulaire et son moment conjugué, les exemples introductifs au cours sont explicites, ainsi que l'exemple qui vient après la seconde propriété du lagrangien.
Tous les types de variables cycliques s'y retrouvent.
Voir la démonstration ci après dans le traitement du problème à deux corps
