Si le lagrangien du système ne dépend pas du temps et les notations suivantes étant assumées :
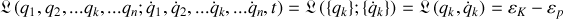
la dérivée temporelle de la fonctionnelle lagrangienne s'écrit :
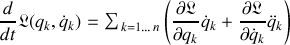
Deux opérations sont effectuées.
Les équations d'Euler Lagrange sont utilisées pour transformer le premier terme, en remplaçant la force généralisée.
La dérivée seconde du second terme s'exprime en fonction de la dérivée première.
Elles permettent d'obtenir :
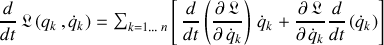
La dérivée temporelle d'un produit apparaît clairement :
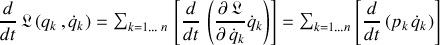
La dérivée temporelle peut être factorisée sur la somme discrète selon :
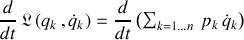
Cette égalité met en évidence une nouvelle fonctionnelle, à l'origine d'une loi de conservation.
Fondamental : Fonction de Hamilton, ou hamiltonien, à partir du lagrangien
Lorsque le lagrangien ne dépend pas explicitement du temps, une nouvelle fonctionnelle apparaît qui possède la propriété d'être conservée :
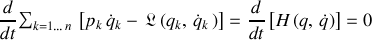
Il s'agit de l'hamiltonien du système, noté
.
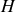À ce stade de l'analyse, cette fonctionnelle dépend des coordonnées et vitesses généralisées.
Cette fonctionnelle sera à l'origine d'un formalisme canonique, lequel sera développé plus loin dans ce cours.
Elle présente un autre intérêt, contenu dans son interprétation physique.
Explication : Hamiltonien et énergie mécanique totale
Un retour vers les grandeurs réelles est nécessaire pour exprimer l'impulsion généralisée.
Si le lagrangien ne dépend pas du temps, la vitesse n'en dépend pas non plus.
Pour chaque particule
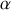, elle s'écrit :
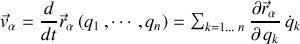
Les notations pour l'énergie cinétique totale étant définie par :
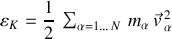
En prenant soin de changer d'indice pour chaque sommation prmettant le passage de la vitesse réelle à celle généralisée, l'énergie cinétique s'écrit :
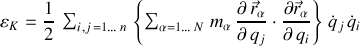
La forme bicarrée en vitesses généralisées apparaît explicitement.
Pour un système conservatif, seule l'énergie cinétique dépend des vitesses généralisées.
Ainsi l'impulsion généralisée peut s'écrire :
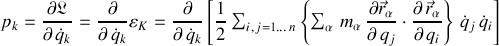
En dérivant par rapport à la vitesse généralisée
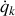, chaque somme discrète apporte la même contribution à l'impulsion généralisée, de sorte que :
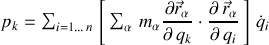
La grandeur
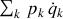apparaissant dans la définition de la fonctionnelle de Hamilton s'écrit finalement :
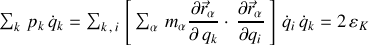
Ainsi cette grandeur
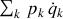contenue dans l'expression de l'hamiltonien vaut le double de l'énergie cinétique.
L'hamiltonien s'écrit alors :
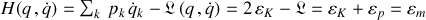
Apparaît l'énergie mécanique totale qui, pour un système conservatif, est l'hamiltonien ou la fonctionnelle de Hamilton du système.
Pour un système conservatif, dont le lagrangien ne dépend pas explicitement du temps, l'énergie mécanique totale est conservée.
Fondamental : Propriété
Le lagrangien d'un système conservatif ne dépend pas explicitement du temps.
Sa fonctionnelle de Hamilton est identique à son énergie mécanique :
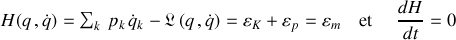
Elle est conservée au cours du temps.
Remarque : Lois de conservations et symétries d'espace.
Précis sur les lois de conservation et relations avec les symétries d'espace.
L'uniformité du temps : le temps
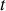est implicite dans la fonctionnelle lagrangienne. - L'énergie totale (et hamiltonien) du système est conservée.
Le système est dit conservatif.
L'homogénéité de l'espace, selon une ou plusieurs directions, exprime une invariance par translation selon la direction.
- La variable d'espace est cyclique car le lagrangien n'en dépend pas explicitement.
L'impulsion selon cette direction d'invariance est conservée.
Lorsque les trois directions de l'espace réel sont invariantes, la description intuitive du mouvement libre est retrouvée.
L'isotropie dans l'espace correspond à une invariance par rotation.
Si une variable angulaire est cyclique, le lagrangien n'en dépend pas explicitement.
La grandeur conservée est le moment cinétique , associé à la rotation concernée et toutes les directions dans le plan perpendiculaire à l'axe de rotation sont équivalentes.
